以三角形的邊為直徑作圓。證明任意兩邊的圓在第三邊（或第三邊的延長線）上相交。

已知

以三角形的邊為直徑作圓。

要證明

我們必須證明任意兩邊的圓在第三邊（或第三邊的延長線）上相交。

解答

在△ABC中，以AB和AC為直徑作圓。

作AD⊥BC

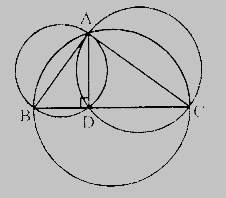
AD⊥BC

這意味著：

∠ADB = ∠ADC = 90°

從圖中可以看出：

以AB和AC為直徑所作的圓將經過D點。

因此，以三角形的兩邊為直徑所作的圓經過位於第三邊的D點。

教程點

更新於：2022年10月10日

76 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習