資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究如果三角形的三條邊的中點分別為$(-2, 3)、(4, -3)$和$(4, 5)$，求該三角形的重心的座標。
已知
三角形三條邊的中點的座標為$(-2, 3)、(4, -3)$和$(4, 5)$。
要求
我們需要找到該三角形的重心的座標。
解答
設$\triangle ABC$的頂點分別為$A (x_1, y_1)、B (x_2, y_2)$和$C (x_3, y_3)$，且$D(-2,3)、E(4,-3)$和$F(4,5)$分別是$BC、CA$和$AB$的中點。
設$G(x,y)$為三角形的重心。
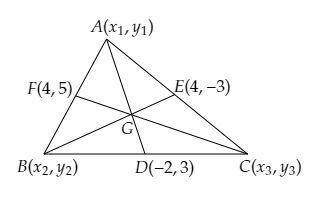
$D$是$BC$的中點。
這意味著，
\( \frac{x_{2}+x_{3}}{2}=-2 \)
\( \Rightarrow x_{2}+x_{3}=-4 \).....(i)
\( \frac{y_{2}+y_{3}}{2}=3 \)
\( \Rightarrow y_{2}+y_{3}=6 \)......(a)
類似地，
\( E \)是\( A C \)的中點。
\( \frac{x_{3}+x_{1}}{2}=4 \)
\( \Rightarrow x_{3}+x_{1}=8 \).......(ii)
\( \frac{y_{3}+y_{1}}{2}=-3 \)
\( \Rightarrow y_{3}+y_{1}=-6 \).......(b)
\( \mathrm{F} \)是\( \mathrm{AB} \)的中點。
\( \frac{x_{2}+x_{1}}{2}=4 \)
\( \Rightarrow x_{2}+x_{1}=8 \)........(iii)
\( \frac{y_{2}+y_{1}}{2}=5 \)
\( \Rightarrow y_{2}+y_{1}=10 \).......(c)
將(i)、(ii)和(iii)相加，得到：
\( 2\left(x_{1}+x_{2}+x_{3}\right)=12 \)
\( \Rightarrow x_{1}+x_{2}+x_{3}=6 \)......(iv)
從(iv)中減去(i)、(ii)和(iii)，得到：
\( x_{1}=10, x_{2}=-2, x_{3}=-2 \)
類似地，
將(a)、(b)和(c)相加，得到：
\( 2\left(y_{1}+y_{2}+y_{3}\right)=10 \)
\( \Rightarrow y_{1}+y_{2}+y_{3}=5 \).......(d)
從(d)中減去(a)、(b)和(c)，得到：
\( y_{1}=-1 \) \( y_{2}=11 \) \( y_{3}=-5 \)
因此，\( \Delta \mathrm{ABC} \)的頂點為\( \mathrm{A}(10,-1), \mathrm{B}(-2,11), \mathrm{C}(-2,-5) \)
我們知道，
三角形重心的座標為$(\frac{橫座標之和}{3}, \frac{縱座標之和}{3})$
因此，
三角形ABC的重心的座標為：
$G(x,y)=(\frac{10-2-2}{3}, \frac{-1+11-5}{3})$
$=(\frac{6}{3}, \frac{5}{3})$
$=(2,\frac{5}{3})$
給定三角形的重心的座標為$(2,\frac{5}{3})$。
171 次檢視
