資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法學下圖顯示了鐵路隧道的橫截面。圓形部分的半徑OA為2米。如果∠AOB=90°，計算隧道的拱高。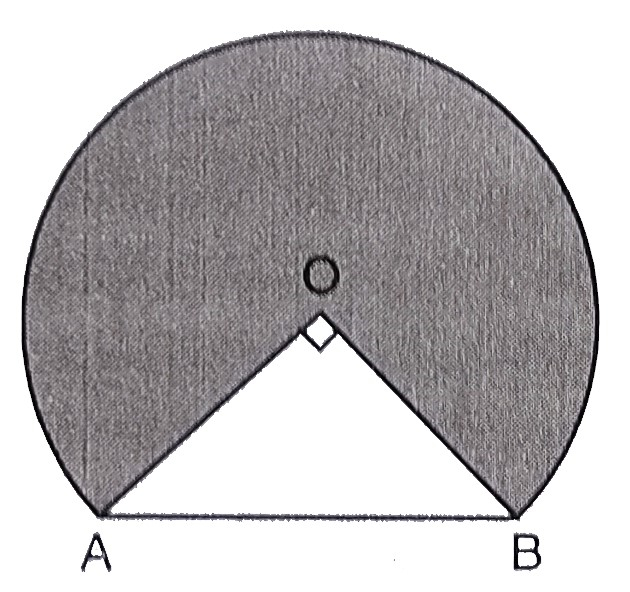
已知
圓形部分的半徑OA為2米。
∠AOB=90°。
要求：
我們需要計算隧道的拱高。
解答
隧道圓形部分的半徑 = 2米
這意味著：
OA = OB = 2米，∠AOB = 90°
作CD⊥AB
D是AB的中點
在直角三角形AOB中，根據勾股定理：
AB² = OA² + OB²
$=2^{2}+2^{2}$
$=4+4$
$=8$
⇒ AB = √8
= √(4 × 2)
= 2√2 米
AD = DB = (2√2)/2 = √2
OD² = OA² - AD²
= 2² - (√2)²
$=4-2$
$=2$
⇒ OD = √2 米
隧道的拱高 = CD
= OC + OD
= (2 + √2) 米
隧道的拱高為(2 + √2)米。
更新於：2022年10月10日
30 次瀏覽
廣告