在一個直徑為 \( 10 \mathrm{~cm} \) 的圓中，畫一條長 \( 6 \mathrm{~cm} \) 的弦。求這條弦到圓心的垂直距離。

已知

一條長 \( 6 \mathrm{~cm} \) 的弦在直徑為 \( 10 \mathrm{~cm} \) 的圓中。

要求

我們必須找到垂直線從圓心到弦的距離。
 解答

設 $AB$ 為弦，$O$ 為圓心，$OC$ 為從 $O$ 到 $AB$ 的垂線。

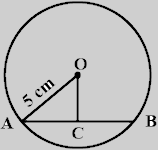
我們知道，

從圓心到弦的垂線平分弦。

因此，

$AC=CB$

$=\frac{6}{2}$

$=3\ cm$

$\triangle OCA$ 是一個直角三角形。

因此，根據勾股定理，

$OA^2 =OC^2 + AC^2$

$OC^2 = 5^2-3^2$

$=25-9$

$=16$

$\Rightarrow OC=\sqrt{16}=4\ cm$

因此，弦到圓心的距離為 $4\ cm$。

教程點

更新於: 2022年10月10日

64 次瀏覽

開啟您的 職業生涯

完成課程，獲得認證

開始學習