一個圓的兩個弦\( \mathrm{AB} \)和\( \mathrm{CD} \)的長度分別為\( 5 \mathrm{~cm} \)和\( 11 \mathrm{~cm} \)，它們互相平行且位於圓心的兩側。如果\( \mathrm{AB} \)和\( C D \)之間的距離為\( 6 \mathrm{~cm} \)，求圓的半徑。

已知

圓的兩條弦$AB$和$CD$的長度分別為$5\ cm$和$11\ cm$，它們互相平行且位於圓心的兩側。

$AB$和$CD$之間的距離為$6\ cm$。

要求

求圓的半徑。

解答

設圓的半徑為$r$，圓心為$O$。


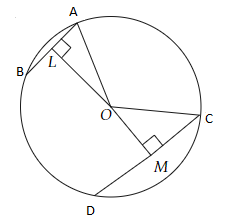
兩條平行弦$AB = 5\ cm, CD = 11\ cm$

設$OL \perp AB$且$OM \perp CD$

$LM = 6\ cm$

設$OM = x$

這意味著，

$OL = 6 - x$

在直角三角形$\mathrm{OAL}$中，

$\mathrm{OA}^{2}=\mathrm{OL}^{2}+\mathrm{AL}^{2}$

$r^{2}=(6-x)^{2}+(\frac{5}{2})^{2}$

$=36-12 x+x^{2}+\frac{25}{4}$............(i)

類似地，

在直角$\Delta \mathrm{OCM}$中，

$r^{2}=x^{2}+(\frac{11}{2})^{2}$

$=x^{2}+\frac{121}{4}$..............(ii)

由(i)和(ii)，得到，

$x^{2}+\frac{121}{4}=36-12 x+x^{2}+\frac{25}{4}$

$\Rightarrow \frac{121}{4}-\frac{25}{4}-36=-12 x$

$\Rightarrow \frac{96}{4}-\frac{36}{1}=-12 x$

$\Rightarrow 12 x=36-24=12$

$x=\frac{12}{12}=1$

$\Rightarrow r^{2}=\mathrm{CM}^{2}+\mathrm{OM}^{2}$

$=(\frac{11}{2})^{2}+(1)^{2}$

$=\frac{121}{4}+1$

$=\frac{125}{4} \mathrm{~cm}$

$\Rightarrow r=\sqrt{\frac{125}{4}}$

$=\frac{\sqrt{125}}{2}$

$=\frac{\sqrt{25 \times 5}}{2}$

$=\frac{5}{2} \sqrt{5} \mathrm{~cm}$

圓的半徑為$\frac{5}{2} \sqrt{5} \mathrm{~cm}$。 

更新於: 2022年10月10日

30 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習
廣告