一個氣球透過一根長為\( 215 \mathrm{~m} \)的纜繩與氣象地面站相連，纜繩與水平面成\( 60^{\circ} \)角。確定氣球離地面的高度。假設纜繩沒有鬆弛。

已知

一個氣球透過一根長為\( 215 \mathrm{~m} \)的纜繩與氣象地面站相連，纜繩與水平面成\( 60^{\circ} \)角。

需要完成

我們需要確定氣球離地面的高度。

解：  

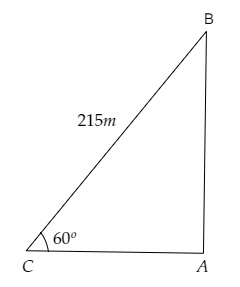
設 $C$ 為氣象地面站，$AB$ 為氣球離地面的高度。

從圖中可以看出，

$\mathrm{BC}=215 \mathrm{~m}, \angle \mathrm{BCA}=60^{\circ}$

設氣球離地面的高度為 $\mathrm{AB}=h \mathrm{~m}$。

我們知道，

$\sin \theta=\frac{\text { 對邊 }}{\text { 斜邊 }}$

$=\frac{\text { AB }}{BC}$

$\Rightarrow \sin 60^{\circ}=\frac{h}{215}$

$\Rightarrow \frac{\sqrt3}{2}=\frac{h}{215}$

$\Rightarrow (215)\frac{\sqrt3}{2}=h \mathrm{~m}$

$\Rightarrow h=\frac{215(1.732)}{2} \mathrm{~m}$

$\Rightarrow h=185.975 \mathrm{~m}$

$\Rightarrow h=186 \mathrm{~m}$

因此，氣球離地面的高度為 $186 \mathrm{~m}$。

教程點

更新於： 2022年10月10日

41 次瀏覽

開啟你的 職業生涯

完成課程獲得認證

開始學習