資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究一棵樹在離地面 5 米高處斷裂，樹頂落到離樹根 12 米處。求這棵樹原來的高度。
已知：一棵樹在離地面 $5\ m$ 高處斷裂，樹頂落到離樹根 $12\ m$ 處。
求解：求這棵樹原來的高度。
解答
設 $ACB$ 表示樹在斷裂點 $C$ 處斷裂前的狀態，設樹頂 $A$ 在斷裂後落到地面上的點為 $A'$。
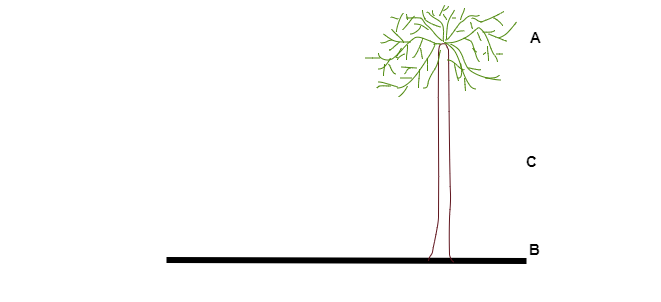
則 $\Delta ABC$ 是一個直角三角形，$\angle B$ 為直角。
$AB=12\ m$
$BC=5\ m$
根據勾股定理，
$(AC)^2=(AB)^2+(BC)^2$
$\Rightarrow (AC)^2=(12)^2+(15)^2$
$\Rightarrow (AC)^{2\ }=144+25$
$\Rightarrow (AC)^2=169$
$AC=13\ m$
因此，樹的總高度
$=AC+CB$
$=13\ m+5\ m=18\ m$
更新於： 2022年10月10日
67 次檢視
廣告