資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學單位衝激函式和單位階躍函式的拉普拉斯變換
拉普拉斯變換
拉普拉斯變換是一種數學工具，用於將時域中的微分方程轉換為頻域或s域中的代數方程。
數學上，如果$\mathit{x}\mathrm{\left(\mathit{t}\right)}$是時域函式，則其拉普拉斯變換定義為：
$$\mathrm{\mathit{L}\mathrm{\left[ \mathit{x}\mathrm{\left(\mathit{t}\right)}\right]}\:\mathrm{=}\:\mathit{X}\mathrm{\left(\mathit{s}\right)}\:\mathrm{=}\:\int_{-\infty}^{\infty}\mathit{x}\mathrm{\left(\mathit{t}\right)}\mathit{e^{-st}}\:\mathit{dt}\:\:\:\:\:\:...(1)}$$
公式(1)給出了函式$\mathit{x}\mathrm{\left(\mathit{t}\right)}$的雙邊拉普拉斯變換。但對於因果訊號，則應用單邊拉普拉斯變換，其定義為：
$$\mathrm{\mathit{L}\mathrm{\left[ \mathit{x}\mathrm{\left(\mathit{t}\right)}\right]}\:\mathrm{=}\:\mathit{X}\mathrm{\left(\mathit{s}\right)}\:\mathrm{=}\:\int_{\mathrm{0}}^{\infty }\mathit{x}\mathrm{\left(\mathit{t}\right)}\mathit{e^{-st}}\:\mathit{dt}\:\:\:\:\:\:...(2)}$$
衝激函式的拉普拉斯變換
衝激函式定義為：
$$\mathrm{\mathit{\delta}\mathrm{\left(\mathit{t}\right)}\mathrm{=}\begin{cases} 1& \text{ 當 } t= 0 \ 0 & \text{ 當 } t
\neq 0 \end{cases}}$$
因此，根據拉普拉斯變換的定義，我們有：
$$\mathrm{\mathit{X}\mathrm{\left(\mathit{s}\right)}\mathrm{=}\mathit{L\mathrm{\left[\mathit{\delta}\mathrm{\left(\mathit{t}\right)} \right]}}\:\mathrm{=}\:\int_{\mathrm{0}}^{\infty}\mathit{\delta}\mathrm{\left(\mathit{t}\right)}\mathit{e^{-st}}\:\mathit{dt}}$$
$$\mathrm{\Rightarrow \mathit{L\mathrm{\left[\mathit{\delta}\mathrm{\left(\mathit{t}\right)}\right]}}\:\mathrm{=}\:\mathrm{\left[\mathit{e^{-st}} \right]_{\mathit{t=\mathrm{0}}}}\:\mathrm{=}\:\mathrm{1}}$$
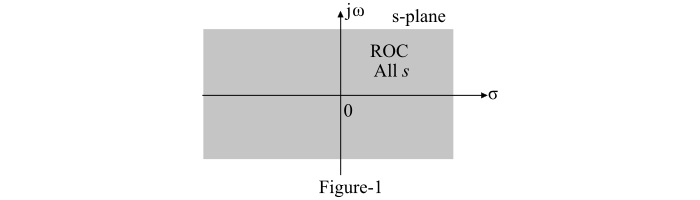
衝激函式拉普拉斯變換的收斂域(ROC)是整個s平面，如圖1所示。因此，衝激函式的拉普拉斯變換及其ROC為：
$$\mathrm{\mathit{\delta}\mathrm{\left(\mathit{t}\right)}\overset{\mathit{LT}}{\leftrightarrow}\mathrm{1}\:\mathrm{且ROC\to 全部}\:\mathit{s}}$$
階躍函式的拉普拉斯變換
單位階躍函式定義為：
$$\mathrm{\mathit{u}\mathrm{\left(\mathit{t}\right)}\mathrm{=}\begin{cases} 1& \text{ 當 } t\geq 0 \ 0 & \text{ 當 } t< 0 \end{cases}}$$
因此，根據拉普拉斯變換的定義，我們得到：
$$\mathrm{\mathit{X}\mathrm{\left(\mathit{s}\right)}\:\mathrm{=}\:\mathit{L\mathrm{\left[\mathit{u}\mathrm{\left(\mathit{t}\right)} \right]}}\:\mathrm{=}\:\int_{\mathrm{0}}^{\infty}\mathit{u}\mathrm{\left(\mathit{t}\right)}\mathit{e^{-st}}\:\mathit{dt}}$$
$$\mathrm{\Rightarrow \mathit{L\mathrm{\left[\mathit{u}\mathrm{\left(\mathit{t}\right)} \right]}}\:\mathrm{=}\:\int_{\mathrm{0}}^{\infty}\mathit{e^{-st}}\:\mathit{dt}\:\mathrm{=}\:\mathrm{\left[\frac{\mathit{e^{-st}}}{-\mathit{s}}\right]^{\infty}_{\mathrm{0}}}}$$
$$\mathrm{\Rightarrow \mathit{L\mathrm{\left[\mathit{u}\mathrm{\left(\mathit{t}\right)} \right]}}\:\mathrm{=}\:\mathrm{\left[\frac{\mathit{e^{-\infty}}-\mathit{e^{\mathrm{0}}}}{-\mathit{s}}\right]\:\mathrm{=}\:\frac{1}{\mathit{s}}}}$$
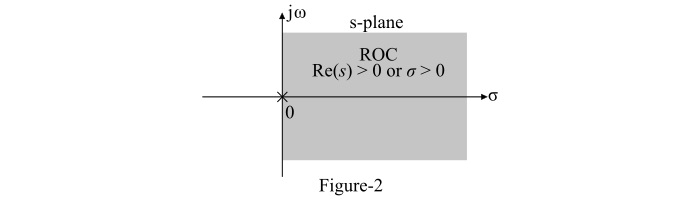
當$\mathit{Re}\mathrm{\left(\mathit{s} \right )}>\mathrm{0}$時，上述積分收斂，即單位階躍函式的拉普拉斯變換的ROC為$\mathit{Re}\mathrm{\left(\mathit{s} \right )}>\mathrm{0}$，如圖2所示。因此，階躍函式的拉普拉斯變換及其ROC為：
$$\mathrm{\mathit{u}\mathrm{\left(\mathit{t}\right)}\overset{\mathit{LT}}{\leftrightarrow}\frac{1}{\mathit{s}}\:\mathrm{且ROC\to Re\mathrm{\left(\mathit{s}\right)}}>\mathrm{0}}$$
17K+ 次瀏覽
