資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物
數學
英語
經濟學
心理學
社會科學
時尚研究
法律研究單位衝激訊號– 定義、波形和屬性
理想的衝激訊號是一種訊號，它在原點 (t = 0) 之外全部為零，它無限高。但是，衝激面積是有限的。單位衝激訊號是分析訊號和系統時使用最廣泛的標準訊號。
連續時間單位衝激訊號
連續時間單位衝激訊號記為 δ(t)，定義為 −
$$\mathrm{\delta (t)=\left\{\begin{matrix} 1\; \; for\: t=0\ 0\; \; for\:t
eq 0 \ \end{matrix}\right.}$$
因此，根據定義，單位衝激訊號在 t = 0 以外的任何地方幅度均為零。在原點 (t = 0) 衝激訊號的幅度無窮大，因此曲線下面積為一。連續時間衝激訊號也稱為狄拉克δ函式。
圖 1 顯示了連續時間單位衝激訊號 δ(t) 的圖形表示。
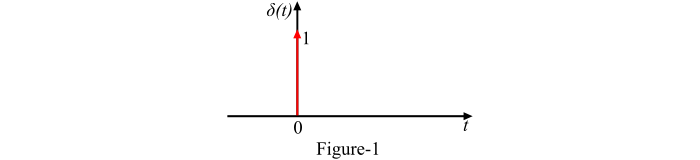
另外，如果單位脈衝訊號以脈衝的形式假設，則關於單位脈衝訊號可以觀察到以下幾點−
脈衝的寬度為零，這意味著脈衝僅存在於原點 (t = 0)。
脈衝的高度為無限大。
曲線下的面積為一。
箭頭的長度表示脈衝曲線下的總面積。
連續時間單位脈衝訊號的特性
連續時間單位脈衝訊號的特性如下所示 −
連續時間單位脈衝訊號是一個偶訊號。這意味著它是時間的偶函式 (t)，即 δ(t) = δ(-t)。
取樣特性：$\mathrm{\int_{-\infty }^{\infty }x(t)\delta (t)dt=x(0)}$
平移特性：$\mathrm{\int_{-\infty }^{\infty }x(t)\delta (t-t_{0})dt=x(t_{0})}$
縮放特性：$\mathrm{\delta(at)=\frac{1}{\left | a \right |}\delta (t) }$
乘法特性：𝑥(𝑡)𝛿(𝑡) = 𝑥(0)𝛿(𝑡) = 𝑥(0); 𝑥(𝑡)𝛿(𝑡 − 𝑡0) = 𝑥(𝑡0)𝛿(𝑡 − 𝑡0)
離散時間單位脈衝訊號
離散時間單位脈衝訊號用 δ(n) 表示，定義為 −
$$\mathrm{\delta(n)=\left\{\begin{matrix} 1\; for\: n=0\ 0\; for\: n
eq 0\ \end{matrix}\right. }$$
離散時間訊號也稱為單位取樣序列。離散時間訊號或單位取樣序列的圖形表示如圖 2 所示。
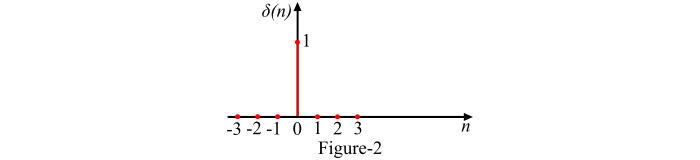
離散時間單位脈衝訊號的特性
離散時間單位脈衝訊號的特性如下 −
$\mathrm{\delta (n)=u(n)-u(n-1)}$
$\mathrm{\delta (n-k)=\left\{\begin{matrix} 1\; \; for\; n=k\ 0\; \; for\; n
eq k\ \end{matrix}\right.}$$\mathrm{x(n)=\sum_{k=-\infty }^{\infty }x(k)\delta (n-k)}$
$\mathrm{\sum_{n=-\infty }^{\infty }x(n)\delta (n-n_{0})=x(n_{0})}$
單位脈衝訊號與單位階躍訊號之間的關係
單位脈衝訊號的時域積分是單位階躍訊號。換句話說，單位階躍訊號的時域導數是單位脈衝訊號，即
$$\mathrm{\int_{-\infty }^{\infty }\delta (t)\: dt=u(t)}$$
及
$$\mathrm{\delta (t)=\frac{\mathrm{d} }{\mathrm{d} t}u(t)}$$
32K+ 次瀏覽
