電導和電導率 – 定義、單位、公式和示例

---

在本文中，我們將討論電導和電導率，包括其定義、公式、測量單位以及已解決的數值示例。

什麼是電導？

衡量電荷（或電子或電流）透過材料的難易程度稱為該材料的電導或電氣電導。

因此，電導定義了物質傳導電的能力。為了理解電導的概念，我們必須回顧材料的電阻。

電阻定義為材料對電流或電荷流動產生的阻礙程度的衡量。電阻主要是由於電荷與材料內部原子離子的碰撞造成的。

因此，在電荷與原子離子碰撞次數較少的材料中，材料的電導會更大，反之亦然，因此，這種材料更容易導電。因此，本次討論表明，電導是與電阻相反的材料屬性。

電導的公式和單位

在電氣和電子電路中，電導定義為導體電阻的倒數。它用符號‘G’表示。

$$\mathrm{\therefore 電導，G\, =\, \frac{1}{電阻\left ( R \right )}\: \: \: \cdot \cdot \cdot \left ( 1 \right )}$$

根據歐姆定律，導體的電阻由下式給出：

$$\mathrm{電阻，R\, =\, \frac{V}{I}}$$

其中，V是導體兩端的電壓，I是透過導體的電流。

$$\mathrm{\therefore G\, =\, \frac{I}{V}\: \: \cdot \cdot \cdot \left ( 2 \right )}$$

此外，導體的電阻可以用導體的物理尺寸表示為：

$$\mathrm{R\, =\, \frac{\rho l}{a}}$$

因此，用導體的物理尺寸表示的電導將是：

$$\mathrm{G\, =\, \frac{a}{\rho l}\, =\, \sigma \frac{a}{ l}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

其中，σ稱為導體材料的電導率或比電導。

$$\mathrm{\therefore \sigma \, =\, \frac{1}{\rho}}$$

電導的單位

由於導體的電導由下式給出：

$$\mathrm{G=\frac{1}{R}=\frac{I}{V}=\frac{\sigma a}{l}}$$

$$\mathrm{\therefore G的單位=\frac{1}{歐姆\, \left ( \Omega \right )}=\frac{安培}{伏特}=姆歐}$$

因此，電導的單位是姆歐 (Ω^-1)。但在實踐中，我們通常使用西門子 (S)作為電導的單位。其中，

$$\mathrm{1\: 姆歐 (\Omega ) = 1\: \: 西門子}$$

影響電導的因素

從公式 (3) 中，我們有：

$$\mathrm{G=\frac{\sigma a}{l}}$$

因此，導體的電導為：

• 與導體的橫截面積成正比。

• 與導體的長度成反比。

• 取決於材料的性質 (σ)。

• 隨溫度變化。

什麼是電導率？

物質提供電流或電荷輕鬆流過它的能力稱為電導率。它用希臘字母 sigma (σ) 表示。

電導率是物質最重要的特性之一，用於選擇合適的材料來製造導體和絕緣體。其中，如果材料具有高電導率，則最適合製造導線，如果材料具有低電導率，則適合製造絕緣體。

基本上，電導率解釋了材料在施加電場時對電流流動的行為。

在數學上，材料的電導率表示為其電阻率的倒數，即：

$$\mathrm{電導率，\sigma =\frac{1}{電阻率\left ( \rho \right )}\cdot \cdot \cdot \left ( 4 \right )}$$

電導率也稱為比電導。電導率的測量單位為西門子每米 (S/m)或姆歐每米 (Ω^-1m^-1)。

串聯電路的電導

考慮圖 1 所示的串聯電阻電路。該電路由三個串聯連線的電阻組成。

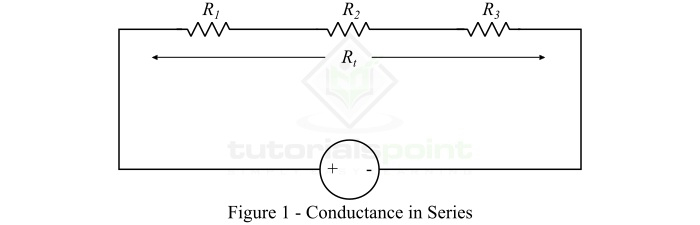
從電路中，我們有：

$$\mathrm{R_{t}=R_{1}\, +\,R_{2}\, +\,R_{3} }$$

$$\mathrm{ \because 電導，G=\frac{1}{R}}$$

因此，

$$\mathrm{ \frac{1}{G_{t}}=\frac{1}{R_{1}}\, +\,\frac{1}{R_{2}}\, +\,\frac{1}{R_{3}}\, \, \cdot \cdot \cdot \left ( 5 \right ) }$$

另外，

$$\mathrm{G_{t}=\frac{1}{R_{t}}=\frac{1}{R_{1}\, +\,R_{2}\, +\,R_{3}} \, \, \cdot \cdot \cdot \left ( 6 \right )}$$

因此，當多個電阻串聯連線時，總電導的倒數等於各個電阻電導的倒數之和。

並聯電路的電導

考慮圖 2 所示的並聯電路。它由三個並聯連線的電阻組成。

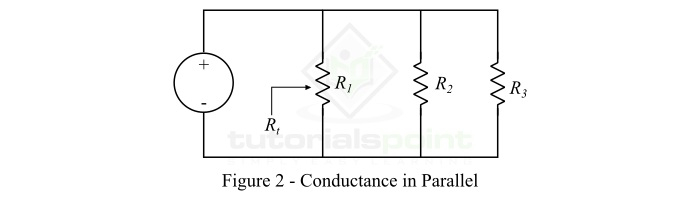
從電路中，我們可以寫出：

$$\mathrm{ \frac{1}{R_{t}}=\frac{1}{R_{1}}\, +\,\frac{1}{R_{2}}\, +\,\frac{1}{R_{3}} }$$

根據電導的定義，我們有：

$$\mathrm{ G=\frac{1}{R}}$$

因此，

$$\mathrm{ G_{t}=G_{1}\, +\,G_{2}\, +\,G_{3}\: \: \cdot \cdot \cdot \left ( 7 \right ) }$$

因此，當多個電阻並聯連線時，電路的總電導等於各個電阻電導之和。

電導與電導率

導體的電導是衡量導體材料允許電流透過的難易程度。而電導率是材料的屬性，根據該屬性，材料提供電流流動的便利性。

數值示例

計算一根 915 米長的導線的電導，該導線具有 0.88 cm² 的均勻橫截面積。該導線由銅製成，其電導率為 5.9 × 10⁵ S/m。

解答

給定資料：

$$\mathrm{長度，l = 915 m }$$

$$\mathrm{橫截面積，a = 0.88\: \: cm^{2} = 0.88 \times 10^{-4}\: m^{2} }$$

$$\mathrm{電導率，\sigma = 5.9\times 10^{5}\: Sm^{-1} }$$

因此，導線的電導將為：

$$\mathrm{G=\frac{\sigma a}{l}=\frac{\left ( 5.9\times 10^{5} \right )\times \left ( 0.88\times 10^{-4} \right )}{\left ( 915 \right )}}$$

$$\mathrm{\therefore G=0.0867\: S}$$