資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究最經濟的功率因數 – 定義、公式和示例
最經濟的功率因數
使功率因數提高到能夠獲得最大淨年節省的數值，稱為最經濟的功率因數。
當用戶提高功率因數時，會導致其最大 kVA 需求減少。因此，在最大需求電費方面將有年度節省。儘管功率因數的改善涉及功率因數校正裝置的資本投資，但使用者每年仍將以年度利息和折舊的形式支出在用於功率因數校正的裝置上進行的投資。因此，淨年節省將等於最大需求電費的年節省減去功率因數校正裝置的年支出。
推導
考慮一個使用者在功率因數為 $\mathrm{cos}\, \phi _{\mathrm{1}}$ 的情況下承受峰值負載 P kW，並且每年每 kVA 的最大需求電費為 Rs x。
假設使用者藉助功率因數校正裝置將功率因數提高到 $\mathrm{cos}\, \phi _{\mathrm{2}}$。假設在功率因數改善裝置上支出的費用為每年每 kVAR Rs y。
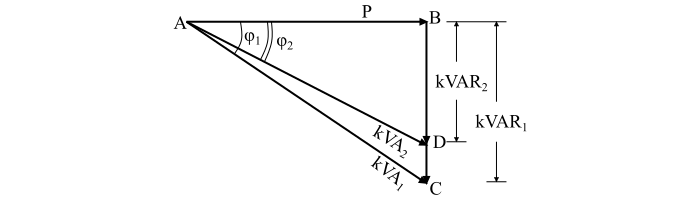
參考圖示，初始功率因數 ($\mathrm{cos}\, \phi _{\mathrm{1}}$)下的功率三角形為 ABC，改進功率因數 ($\mathrm{cos}\, \phi _{\mathrm{2}}$)下的功率三角形為 ABD。
因此，原始功率因數下的最大 kVA 需求為：
$$\mathrm{\mathit{kV\, A_{\mathrm{1}}\mathrm{\, =\, }\frac{P}{\mathrm{cos}\, \phi _{\mathrm{1}}}\mathrm{\, =\, }P\, \mathrm{sec}\, \phi _{\mathrm{1}}}}$$
改進功率因數下的最大 kVA 需求由下式給出：
$$\mathrm{\mathit{kV\, A_{\mathrm{2}}\mathrm{\, =\, }\frac{P}{\mathrm{cos}\, \phi _{\mathrm{2}}}\mathrm{\, =\, }P\, \mathrm{sec}\, \phi _{\mathrm{2}}}}$$
然後，每年最大需求電費的節省為：
$$\mathrm{每年節省\mathrm{\, =\, } \mathit{Rs.x\left (kV\, A_{\mathrm{1}}-kV\, A_{\mathrm{2}} \right )}}$$
$$\mathrm{\Rightarrow 每年節省\mathrm{\, =\, } \mathit{Rs.x\left (\frac{P}{\mathrm{cos}\, \phi _{\mathrm{1}}}-\frac{P}{\mathrm{cos}\, \phi _{\mathrm{2}}} \right )}}$$
$$\mathrm{\Rightarrow 每年節省\mathrm{\, =\, } \mathit{Rs.xP\left (\mathrm{sec}\, \phi _{\mathrm{1}}- \mathrm{sec}\, \phi _{\mathrm{2}} \right )}\; \; \cdot \cdot \cdot \left ( 1 \right )}$$
此外，原始功率因數下的無功功率為：
$$\mathrm{kVAR_{\mathrm{1}}\mathit{\mathrm{\, =\, }P\, \mathrm{tan}\, \phi _{\mathrm{1}}}}$$
改進功率因數下的無功功率為：
$$\mathrm{kVAR_{\mathrm{2}}\mathit{\mathrm{\, =\, }P\, \mathrm{tan}\, \phi _{\mathrm{2}}}}$$
功率因數校正裝置產生的超前無功功率由下式給出：
$$\mathrm{\mathrm{\, =\, }kVAR_{\mathrm{1}}-kVAR_{\mathrm{2}} \mathit{\mathrm{\, =\, }P \left ( \mathrm{tan}\, \phi _{\mathrm{1}}-\mathrm{tan}\, \phi _{\mathrm{2}} \right )}}$$
因此，功率因數校正裝置的年成本為：
$$\mathrm{裝置年成本\mathrm{\, =\, }Rs\, \mathit{yP \left ( \mathrm{tan}\, \phi _{\mathrm{1}}-\mathrm{tan}\, \phi _{\mathrm{2}} \right )}\: \: \cdot \cdot \cdot \left ( 2 \right )}$$
因此，根據公式 (1) 和 (2)，淨年節省為：
$$\mathrm{\mathit{S\mathrm{\, =\, }xP\left (\mathrm{sec}\, \phi _{\mathrm{1}}- \mathrm{sec}\, \phi _{\mathrm{2}}\right )-yP\left ( \mathrm{tan}\, \phi _{\mathrm{1}}-\mathrm{tan}\, \phi _{\mathrm{2}} \right )}}$$
現在，如果
$$\mathrm{\mathit{\frac{d\left ( S \right )}{d\, \phi \mathrm{2}}}\mathrm{\, =\, }0}$$
則淨年節省將最大。
$$\mathrm{\Rightarrow \mathit{\frac{d}{d\, \phi _{\mathrm{2}}}\left [ xP\left (\mathrm{sec}\, \phi _{\mathrm{1}}- \mathrm{sec}\, \phi _{\mathrm{2}}\right )-yP\left ( \mathrm{tan}\, \phi _{\mathrm{1}}-\mathrm{tan}\, \phi _{\mathrm{2}} \right ) \right ]}\mathrm{\, =\, }0}$$
$$\mathrm{\Rightarrow \mathit{P\left [ \frac{d}{d\, \phi _{\mathrm{2}}}\left ( x\, \mathrm{sec}\, \phi _{\mathrm{1}} \right )-\frac{d}{d\, \phi _{\mathrm{2}}}\left (x\, \mathrm{sec}\, \phi _{\mathrm{2}} \right )-\frac{d}{d\, \phi _{\mathrm{2}}}\left ( y\, \mathrm{tan}\, \phi _{\mathrm{1}} \right )\mathrm{\, +\, }\frac{d}{d\, \phi _{\mathrm{2}}}\left ( y\, \mathrm{tan}\, \phi _{\mathrm{2}} \right ) \right ]}\mathrm{\, =\, }0}$$
$$\mathrm{\Rightarrow 0-\mathit{x\, \mathrm{sec}\, \phi _{\mathrm{2}}\, \mathrm{tan}\, \phi _{\mathrm{2}}-\mathrm{0}\mathrm{\, +\, }y\, \mathrm{sec^{2}}\, \phi _{\mathrm{2}}}\mathrm{\, =\, }0}$$
$$\mathrm{\Rightarrow \mathit{\mathrm{tan}\, \phi _{\mathrm{2}}\mathrm{\, =\, }\frac{y}{x}\mathrm{sec}\, \phi _{\mathrm{2}}}}$$
$$\mathrm{\Rightarrow \mathit{\frac{\mathrm{tan}\, \phi _{\mathrm{2}}}{\mathrm{sec}\, \phi _{\mathrm{2}}}\mathrm{\, =\, }\mathrm{sin}\, \phi _{\mathrm{2}}\mathrm{\, =\, }\frac{y}{x}}}$$
因此，最經濟的功率因數由下式給出：
$$\mathrm{\mathit{\mathrm{cos}\, \phi _{\mathrm{2}}\mathrm{\, =\, } \sqrt{\mathrm{1}-\mathrm{sin^{\mathrm{2}}}\, \phi _{\mathrm{2}}} \mathrm{\, =\, }\sqrt{\mathrm{1}-\left ( \frac{y}{x} \right )^{\mathrm{2}}} }\; \; \cdot \cdot \cdot \left ( 3 \right )}$$
根據公式 (3)，很明顯，最經濟的功率因數與原始功率因數無關。
數值示例
一家造紙廠的最大需求為 185 kW，功率因數為 0.8 滯後，每年每 kVA 的電費為 Rs 75。如果功率因數校正裝置的成本為每 kVAR Rs 130。那麼，工廠應以哪種最經濟的功率因數執行？功率因數校正裝置的利息和折舊費用為其資本投資的 10%。
解決方案
造紙廠的原始功率因數為：
$$\mathrm{\mathit{\mathrm{cos}\, \phi _{\mathrm{1}}}\mathrm{\, =\, }0.8 \, \, 滯後}$$
最大需求電費為
$$\mathrm{\mathit{x\mathrm{\, =\, }𝑅𝑠.}\,75\: 每\: kVA\: 每年 }$$
相位校正裝置的支出為：
$$\mathrm{\mathit{y\mathrm{\, =\, }𝑅𝑠.}\,130\times 10\%\mathrm{\, =\, }\mathit{Rs.}\, 13\: 每\: kVA\: 每年 }$$
因此，工廠的最經濟功率因數為：
$$\mathrm{\mathit{\mathrm{cos}\, \phi _{\mathrm{2}}\mathrm{\, =\, }\sqrt{\mathrm{1}-\left ( \frac{y}{x} \right )^{\mathrm{2}}}\mathrm{\, =\, }\mathrm{\sqrt{1-\left ( \frac{13}{75} \right )^{2}}}}}$$
4K+ 次瀏覽
