電阻溫度係數——定義、公式及示例

---

電氣和電子元件，如電阻器、電容器、電感器、導線、電纜、絕緣體等，由不同型別的材料製成。我們通常將所有這些材料稱為工程材料。根據電阻率，工程材料分為三大類：導體、半導體和絕緣體。

由於自然界中每種材料都具有有限的電阻。而且，這種電阻會隨著溫度的變化而變化。以下幾點簡要說明了不同型別材料的電阻隨溫度變化而變化的情況：

• 導體的電阻隨溫度升高而增加。
• 半導體的電阻隨溫度升高而降低。
• 絕緣材料的電阻也隨溫度升高而降低。

材料電阻隨溫度變化的變化用電阻溫度係數表示。

在本文中，我們將討論電阻溫度係數，包括其定義、推導、公式和示例。讓我們從電阻溫度係數的定義開始。

什麼是電阻溫度係數？

材料電阻隨溫度每單位變化而變化的量稱為電阻溫度係數。它用希臘字母 alpha (α) 表示。

實驗發現，在正常的溫度範圍內：

• 電阻變化與初始電阻成正比，即：

$$\mathrm{\Delta R\propto R_{0}}$$

其中，

$$\mathrm{\Delta R=R_{t}- R_{0}}$$

而 𝑅₀ 是材料的初始電阻，𝑅_t 是材料在任何 t °C 時的電阻。

• 電阻變化與溫度升高成正比，即：

$$\mathrm{\Delta R\propto t-0=t}$$

• 電阻變化取決於材料的性質。

結合前兩點，我們有：

$$\mathrm{\Delta R\propto R_{0}t}$$

$$\mathrm{\Rightarrow \Delta R=\alpha _{0} R_{0}t\: \cdot \cdot \cdot \left ( 1 \right )}$$

此外，

$$\mathrm{R_{t}-R_{0}=\alpha _{0}R_{0}t\: \cdot \cdot \cdot \left ( 2 \right )}$$

或者，

$$\mathrm{R_{t}=R_{0}\left ( 1+\alpha _{0}t \right )\: \cdot \cdot \cdot \left ( 3 \right )}$$

其中，α₀ 是比例常數，稱為材料在 0 °C 時的電阻溫度係數。

重新排列方程 (2)，我們得到：

$$\mathrm{\alpha _{0}=\frac{R_{t}-R_{0}}{R_{0}t}\: \cdot \cdot \cdot \left ( 4 \right )}$$

因此，材料的電阻溫度係數是指溫度每變化 1 °C 時，每歐姆初始電阻的電阻變化量。溫度係數的單位為攝氏度倒數 (°C^-1)。

由於在 0 °C 時的電阻溫度係數 (α₀) 的值對於不同的材料是不同的。因此，對於相同的溫度變化，不同材料的電阻變化也不同。這就是為什麼導體、半導體和絕緣體在相同的溫度變化下顯示出不同的電阻變化。

對於導體，ΔR 的值為正，即導體的電阻隨溫度升高而增加。因此，導體的電阻溫度係數為正。但是，半導體和絕緣體的電阻隨溫度升高而降低。因此，半導體和絕緣體的電阻溫度係數為負。

電阻溫度係數的圖形確定法

我們也可以藉助物質的溫度-電阻圖來圖形化地確定電阻溫度係數的值。考慮圖 1 所示的導體的典型溫度-電阻圖。

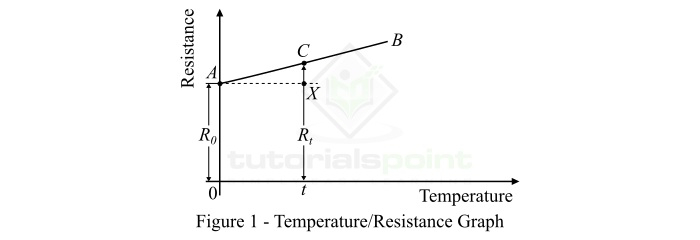
對於導體，溫度-電阻圖的曲線是一條直線。這裡，導體在 0 °C 時的電阻為 𝑅₀，由 OA 表示。導體在 t °C 時的電阻為 R_t。

因此，根據電阻溫度係數的定義，我們有：

$$\mathrm{\alpha _{0}=\frac{R_{t}-R_{0}}{R_{0}\times t}}$$

從溫度-電阻圖，

$$\mathrm{R_{t}-R_{0}=XC}$$

並且，

$$\mathrm{溫度升高=t=AX}$$

因此，導體在 0 °C 時的電阻溫度係數為：

$$\mathrm{\alpha _{0}=\frac{XC}{R_{0}\times AX}}$$

但是，溫度-電阻圖的斜率為：

$$\mathrm{圖的斜率=\frac{XC}{AX}}$$

因此，

$$\mathrm{\alpha _{0}=\frac{溫度-電阻圖的斜率}{初始電阻}\: \cdot \cdot \cdot \left ( 5 \right )}$$

因此，物質在 0 °C 時的電阻溫度係數是溫度-電阻圖的斜率除以物質的初始電阻（或 0 °C 時的電阻，即 𝑅₀）。

任意溫度下的電阻溫度係數

對於一種材料，如果已知其在 0 °C 時的電阻溫度係數（即 α₀）。那麼，我們可以用以下表達式確定該材料在任何溫度下的電阻溫度係數：

$$\mathrm{\alpha _{t}=\frac{\alpha _{0}}{1+\alpha _{0}t}\: \cdot \cdot \cdot \left ( 6 \right )}$$

其中，α_t 是 t °C 時的電阻溫度係數。

注意 − 電阻溫度係數有助於我們確定材料在不同溫度下的電阻值。設 𝑅₁ 和 𝑅₂ 分別是在 𝑡₁°C 和 𝑡₂°C 時材料的電阻。如果 α₁ 是 𝑡₁°C 時的電阻溫度係數。則材料的電阻 R₂ 為：

$$\mathrm{R_{2}=R_{1}\left [ 1+\alpha _{1}\left ( t_{2}-t_{1} \right ) \right ]\: \cdot \cdot \cdot \left ( 7 \right )}$$

一些材料的電阻溫度係數

下表列出了標準溫度 (20 °C) 下一些材料的電阻溫度係數的值，這些材料用於電氣、電子和其他工程領域：

序號	材料	20 °C 時的電阻溫度係數 (°C-1)
6.	鐵 (Fe)	0.00651
12.	鎳 (Ni)	0.00641
5.	鎢 (W)	0.0045
4.	鋁 (Al)	0.00429
13.	錫 (Sn)	0.0042
7.	鉑 (Pt)	0.003927
2.	銅 (Cu)	0.00386
1.	銀 (Ag)	0.0038
3.	金 (Au)	0.0034
8.	汞 (Hg)	0.0009
14.	鎳鉻合金 (Ni-Cr-Fe)	0.0004
16.	康銅 (Cu-Ni)	0.00003
15.	錳銅 (Cu-Mn-Ni)	0.000002
9.	碳 (C)	-0.0005
10.	鍺 (Ge)	-0.05
11.	矽 (Si)	-0.07

數值示例 (1)

一臺電動機的勵磁繞組在 0 °C 時電阻為 15 Ω，在 30 °C 時電阻為 18 Ω。求勵磁繞組在 0 °C 時的電阻溫度係數。

解答

已知資料：

• 𝑅₀ = 15 Ω
• 𝑅₃₀ = 18 Ω

由於在 0 °C 時的電阻溫度係數由下式給出：

$$\mathrm{\alpha _{0}=\frac{R_{t}-R_{0}}{R_{0}\times t}}$$

在本例中，t = 30 °C，因此：

$$\mathrm{\alpha _{0}=\frac{R_{30}-R_{0}}{R_{0}\times 30}=\frac{18-15}{15\times 30}}$$

$$\mathrm{\therefore \alpha _{0}=0.00667\: _{}^{\circ }\textrm{C}^{-1}}$$

數值示例 (2)

一臺直流發電機的分流繞組由銅線製成，在 0 °C 時的電阻溫度係數為 0.00426 °C^-1。確定該繞組在 27 °C 時的電阻溫度係數。

解答

已知資料：

• 𝛼₀ = 0.00426

27 °C 時的電阻溫度係數由下式給出：

$$\mathrm{ \alpha _{27}=\frac{\alpha _{0}}{1+27\alpha _{0}}}$$

$$\mathrm{\Rightarrow \alpha _{27}=\frac{0.00426}{1+\left ( 27\times 0.00426 \right )}}$$

$$\mathrm{\therefore \alpha _{27}=0.00382\, _{}^{\circ }\textrm{C}^{-1}}$$

數值示例 (3)

一臺電動機的定子繞組在 17 °C 時的電阻為 90 Ω。如果其在 17 °C 時的電阻溫度係數為 0.003，求其在 50 °C 時的電阻。

解答

已知資料：

• 𝑅₁₇ = 90 Ω
• 𝛼₁₇ = 0.003

則該繞組在 50 °C 時的電阻由下式給出：

$$\mathrm{R_{50}=R_{17}\left [ 1+\alpha _{17}\left ( 50-17 \right ) \right ]}$$

$$\mathrm{\Rightarrow R_{50}=90\times \left [ 1+0.003\times 33 \right ]}$$

$$\mathrm{\therefore R_{50}=98.91\, \Omega }$$

結論

我們將以以下幾點結束本文：

• 材料的電阻會隨著溫度的變化而變化。

• 材料電阻的變化由一個稱為材料電阻溫度係數的因素來描述。

• 電阻溫度係數有助於我們選擇適合特定應用的材料。

• 電阻溫度係數也可用於確定材料在特定溫度下的電阻。

• 對於金屬，電阻溫度係數為正，這表明金屬的電阻隨著溫度的升高而增加，反之亦然。

對於半導體和絕緣體，電阻溫度係數為負，這表明半導體和絕緣體的電阻隨著溫度的升高而降低，反之亦然。