什麼是磁導——定義、公式、單位、係數和示例

---

在本文中，我們將學習磁路中的磁導，包括其定義、公式、測量單位和係數。

什麼是磁導？

磁通量透過磁性材料的容易程度的量度稱為磁導。它用符號 P 表示，由以下表達式給出：

$$\mathrm{磁導，P=\frac{1}{磁阻}\: \: \cdot \cdot \cdot \left ( 1 \right )}$$

因此，磁導也可以定義為磁阻的倒數。其中，磁阻是磁性材料或磁路對磁通路徑的阻礙程度的量度。

實驗觀察到，磁性材料的磁導與其透過的磁通量成正比，與其磁動勢 (MMF) 成反比。因此，我們有：

$$\mathrm{P=\frac{\phi }{NI}\: \: \cdot \cdot \cdot \left ( 2 \right )}$$

此表示式表明，如果磁路的磁導較低，則需要較大的磁動勢才能在其內部建立一定的磁通量。

磁路的磁導也可以用電路的物理引數表示為：

$$\mathrm{P=\frac{\mu A }{l}=\frac{\mu_{0}\mu_{r} A }{l}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

其中：

• A 是電路的橫截面積；
• l 是磁路的平均長度；
• $\mathrm{\mu_{0}}$ 是自由空間的磁導率，等於 4π × 10^-7 H/m；以及
• $\mathrm{\mu_{r}}$ 是磁性材料的相對磁導率。

因此，從這個等式可以看出，磁路的磁導隨著橫截面積的增加而增加，隨著磁路長度的增加而減少。

磁導的單位是什麼？

由於磁導由磁路中的磁通量與建立此磁通量所需的磁動勢之比給出，即：

$$\mathrm{P=\frac{磁通量}{磁動勢}=\frac{韋伯}{安培匝}}$$

因此，磁導的測量單位為韋伯每安培匝 (Wb/AT)。

此外：

$$\mathrm{1\: Wb/AT = 1\: 亨利 (H)}$$

什麼是磁導係數？

在 B-H 曲線的操作點上，磁通密度與磁場強度之比稱為磁導係數。它通常用符號 P_C 表示。

$$\mathrm{磁導係數，P_{c} = \frac{B_{0}}{H_{0}}\: \: \:\cdot \cdot \cdot \left ( 4 \right )}$$

其中，B₀ 是磁通密度，H₀ 是 B-H 曲線工作點的磁場強度。

磁導係數是磁路設計中的重要引數之一，因為它用於確定磁路在 B-H 曲線上的工作點。

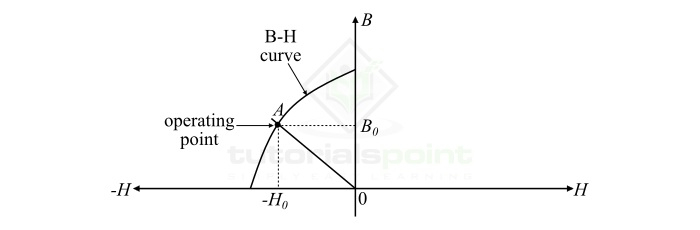
圖中顯示了典型的 B-H 曲線。此處，透過原點的直線 OA 與 B-H 曲線相交於點 A，該點稱為磁路的工作點。線 OA 稱為磁導線，磁導線 OA 的斜率（即 B₀ / H₀）稱為磁導係數。

數值示例

一個磁路由一個橫截面積為 9 cm² 的鐵芯構成。磁路的平均長度為 20 cm，鐵芯材料的相對磁導率為 1000。求磁路的磁導。

解答

已知資料：

$$\mathrm{橫截面積，A = 9\, cm^2 = 9 \times 10^{-4}\, m}$$

$$\mathrm{電路平均長度，l = 20\, cm = 20 \times 10^{-2} m}$$

$$\mathrm{相對磁導率，\mu _{r} = 1000}$$

則磁路的磁導由下式給出：

$$\mathrm{P=\frac{\mu _{0}\mu _{r}A}{l}}$$

$$\mathrm{\Rightarrow P=\frac{(4\pi \times 10^{-7}) \times (1000) \times (9 \times 10^{-4})}{(20 \times 10^{-2})}=5.652 \times 10^{-6} \: Wb/AT}$$