資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律利用拉普拉斯變換分析串聯RL電路的階躍響應和衝激響應
圖1所示為一個由電阻(R)和電感(L)串聯組成的電路。假設開關(S)在時間$\mathrm{\mathit{ t=\mathrm{0}}}$時閉合。
串聯RL電路的階躍響應
為了得到串聯RL電路的階躍響應，施加到電路的輸入$\mathrm{\mathit{x\left ( t \right )}}$由下式給出：
$$\mathrm{\mathit{x\left ( t \right )\mathrm{=}Vu\left ( t \right )}}$$
現在，根據基爾霍夫電壓定律(KVL)，我們得到以下微分方程：
$$\mathrm{\mathit{Vu\left ( t \right )\mathrm{=}Ri\left ( t \right )\mathrm{+}L\frac{di\left ( t \right )}{dt}}}$$
對兩邊進行拉普拉斯變換，得到：
$$\mathrm{\mathit{\frac{V}{s}\mathrm{=}RI\left ( s \right )\mathrm{+}L\left [ sI\left ( s \right )-i\left ( \mathrm{0}^{-} \right ) \right ]}}$$
電感中的電流不能突變。因此，在$\mathrm{\mathit{ t\mathrm{=}\mathrm{0}}}$之前，電路中的電流為零，即電感中的初始電流為$\mathrm{\mathit{i\left ( \mathrm{0}^{-} \right )\mathrm{=}\mathrm{0}}}$。於是：
$$\mathrm{\mathit{\frac{V}{s}\mathrm{=}RI\left ( s \right )\mathrm{+}sLI\left ( s \right )}}$$
$$\mathrm{\Rightarrow \mathit{\frac{V}{s}\mathrm{=}\left ( R\mathrm{+}sL \right )I\left ( s \right )}}$$
因此，電路電流由下式給出：
$$\mathrm{\Rightarrow \mathit{I\left ( s \right )\mathrm{=}\frac{V}{s\left ( R\mathrm{+}sL \right )}}}$$
$$\mathrm{\Rightarrow \mathit{I\left ( s \right )\mathrm{=}\frac{V}{L}\left [ \frac{\mathrm{1}}{s\left ( s\mathrm{+}\frac{R}{L} \right )} \right ]\mathrm{=}\frac{V}{L}\cdot \frac{L}{R}\left [ \frac{\mathrm{1}}{s}-\frac{\mathrm{1}}{\left ( s\mathrm{+}\frac{R}{L} \right )} \right ]}}$$
$$\mathrm{\Rightarrow \mathit{I\left ( s \right )\mathrm{=}\frac{V}{R}\left [ \frac{\mathrm{1}}{s}-\frac{\mathrm{1}}{\left ( s\mathrm{+}\frac{R}{L} \right )} \right ]}}$$
對上述方程進行拉普拉斯反變換，得到：
$$\mathrm{\mathit{i\left ( t \right )\mathrm{=}\frac{V}{R}\left [ \mathrm{1}-e^{-\left (R/L \right )t} \right ]}}$$
這就是串聯RL電路的階躍響應。
串聯RL電路的衝激響應
為了得到串聯RL電路(圖1所示)的衝激響應，施加到電路的輸入$\mathrm{\mathit{x\left ( t \right )}}$由下式給出：
$$\mathrm{\mathit{x\left ( t \right )\mathrm{=}\delta \left ( t \right )}}$$
根據KVL，得到電路的以下微分方程：
$$\mathrm{\mathit{\delta \left ( t \right )\mathrm{=}Ri\left ( t \right )\mathrm{+}L\frac{di\left ( t \right )}{dt}}}$$
對兩邊進行拉普拉斯變換，得到：
$$\mathrm{\mathit{\mathrm{\mathbf{L}}\left [ \delta \left ( t \right ) \right ]\mathrm{=}\mathrm{\mathbf{L}}\left [ Ri\left ( t \right ) \right ]\mathrm{+}\mathrm{\mathbf{L}}\left [ L\frac{di\left ( t \right )}{dt} \right ]}}$$
(L為拉普拉斯變換運算元，$\mathrm{\mathit{L}}$為電感的電感量)
$$\mathrm{\mathit{\Rightarrow \mathrm{1}\mathrm{=}RI\left ( s \right )\mathrm{+}L\left [ sI\left ( s \right )-i\left ( \mathrm{0}^{-} \right ) \right ]}}$$
忽略初始條件，即$\mathrm{\mathit{i\left ( \mathrm{0}^{-} \right )\mathrm{=}\mathrm{0}}}$。則：
$$\mathrm{\mathit{\left ( R\mathrm{+}sL \right )I\left ( s \right )\mathrm{=}\mathrm{1}}}$$
因此，對於衝激輸入，RL串聯電路中的電流為：
$$\mathrm{\mathit{I\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{\left ( R\mathrm{+}sL \right )}\mathrm{=}\frac{\mathrm{1}}{L\left ( s\mathrm{+}\frac{R}{L} \right )}}}$$
進行拉普拉斯反變換，得到：
$$\mathrm{\mathit{L^{-\mathrm{1}}\left [ I\left ( s \right ) \right ]\mathrm{=}L^{-\mathrm{1}}\left [ \frac{\mathrm{1}}{L\left ( s\mathrm{+}\frac{R}{L} \right )} \right ]}}$$
$$\mathrm{\mathit{\therefore i\left ( t \right )\mathrm{=}\frac{\mathrm{1}}{L}e^{-\left ( R/L \right )t}u\left ( t \right )}}$$
這就是串聯RL電路的衝激響應。
數值示例
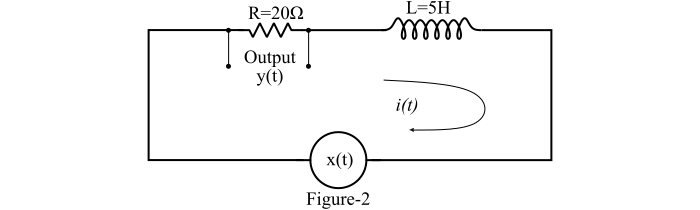
求圖2所示串聯RL電路的階躍響應和衝激響應。
解答
描述圖2所示串聯RL電路的微分方程為：
$$\mathrm{\mathit{x\left ( t \right )\mathrm{=}\mathrm{20}i\left ( t \right )\mathrm{+}\mathrm{5}\frac{di\left ( t \right )}{dt}}}$$
對兩邊進行拉普拉斯反變換，得到：
$$\mathrm{\mathit{X\left ( s \right )\mathrm{=}\mathrm{20}I\left ( s \right )\mathrm{+}\mathrm{5}\left [ sI\left ( s \right )-i\left ( \mathrm{0}^{-} \right ) \right ]}}$$
忽略電路的初始條件，得到：
$$\mathrm{\mathit{X\left ( s \right )\mathrm{=}\mathrm{20}I\left ( s \right )\mathrm{\: +\: }\mathrm{5} sI\left ( s \right )\mathrm{=}\mathrm{5}I\left ( s \right )\left ( s\mathrm{\: +\: }\mathrm{4} \right )}}$$
$$\mathrm{\mathit{\therefore I\left ( s \right )\mathrm{=}\frac{X\left ( s \right )}{\mathrm{5}\left ( s\mathrm{\: +\: }\mathrm{4} \right )}}}$$
參考圖2的電路，電路的輸出為：
$$\mathrm{\mathit{Y\left ( s \right )\mathrm{=}\mathrm{20}I\left ( s \right )\mathrm{=}\mathrm{20}\left [ \frac{X\left ( s \right )}{\mathrm{5}\left ( s\mathrm{\: +\: }\mathrm{4} \right )} \right ]}}$$
$$\mathrm{\mathit{\Rightarrow Y\left ( s \right )\mathrm{=}\left [ \frac{\mathrm{4}}{\left ( s\mathrm{\: +\: }\mathrm{4} \right )} \right ]X\left ( s \right )}}$$
對於單位階躍響應
$$\mathrm{輸入,\mathit{x\left ( t \right )\mathrm{=}u\left ( t \right )}}$$
$$\mathrm{\mathit{\therefore X\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{s}}}$$
因此，電路的輸出為：
$$\mathrm{\mathit{Y\left ( s \right )\mathrm{=}\left [ \frac{\mathrm{4}}{\left ( s\mathrm{\: +\: }\mathrm{4} \right )} \right ]\left ( \frac{\mathrm{1}}{s} \right )\mathrm{=}\frac{\mathrm{4}}{s\left ( s\mathrm{\: +\: }\mathrm{4} \right )}}}$$
$$\mathrm{\mathit{\Rightarrow Y\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{s}-\frac{\mathrm{1}}{\left ( s\mathrm{\: +\: }\mathrm{4} \right )}}}$$
進行拉普拉斯反變換，電路的階躍響應由下式給出：
$$\mathrm{\mathit{L^{-\mathrm{1}}\left [ Y\left ( s \right ) \right ]\mathrm{=}L^{-\mathrm{1}}\left [ \frac{\mathrm{1}}{s} \right ]-L^{-\mathrm{1}}\left [ \frac{\mathrm{1}}{\left ( s\mathrm{\, +\,}\mathrm{4} \right )} \right ]}}$$
$$\mathrm{\mathit{\Rightarrow y\left ( t \right )\mathrm{=}u\left ( t \right )-e^{-\mathrm{4}t}u\left ( t \right )}}$$
$$\mathrm{\mathit{\therefore y\left ( t \right )\mathrm{=}u\left ( t \right )\left [\mathrm{1} -e^{-\mathrm{4}t} \right ]}}$$
對於衝激響應
$$\mathrm{\mathit{x\left ( t \right )\mathrm{=}\delta \left ( t \right )}}$$
$$\mathrm{\mathit{\therefore X\left ( s \right )\mathrm{=}\mathrm{1}}}$$
$$\mathrm{輸出,\mathit{ Y\left ( s \right )\mathrm{=}\left [ \frac{\mathrm{4}}{\left ( s\mathrm{\, +\,}\mathrm{4} \right )} \right ]\left ( \mathrm{1} \right )\mathrm{=}\frac{\mathrm{4}}{\left ( s\mathrm{\, +\,}\mathrm{4} \right )}}}$$
進行拉普拉斯反變換，電路的衝激響應由下式給出：
$$\mathrm{\mathit{ y\left ( t \right )\mathrm{=}\mathrm{4}e^{-\mathrm{4}t}u\left ( t \right )}}$$
10K+ 瀏覽量
