在給定的圖形中，$PS$是$∆PQR$的$\angle QPR$的角平分線。證明$\frac{QS}{SR}=\frac{PQ}{PR}$
"

已知

$PS$是$∆PQR$的$\angle QPR$的角平分線。

需要證明

我們需要證明$\frac{QS}{SR}=\frac{PQ}{PR}$

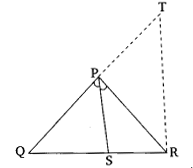
作$RT \parallel PS$，交$QP$的延長線於$T$。

$PS \parallel RT$

這意味著：

$\angle 2=\angle 3$ (內錯角)

$\angle 1=\angle 4$ (同位角)

$\angle 1 = \angle 2$ ($AD$是$\angle A$的角平分線)

因此：

$\angle 3 =\angle 4$

這意味著：

$PT=PR$

在$\triangle QRT$中：

$\frac{QS}{SR}=\frac{PQ}{PT}$

$\frac{QS}{SR}=\frac{PQ}{PR}$

證畢。

Tutorialspoint

更新於：2022年10月10日

瀏覽量：57

開啟你的職業生涯

完成課程獲得認證

開始學習