△ABC是一個三角形。過B點的外部角的角平分線與∠C的角平分線相交於點D。證明∠D = 1/2∠A。

已知

△ABC是一個三角形。過B點的外部角的角平分線與∠C的角平分線相交於點D。

要求

我們必須證明∠D = 1/2∠A。

解答

在△ABC中，CB延長至E。

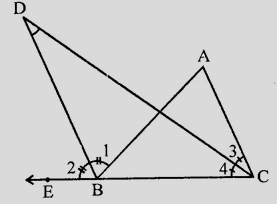
∠ABE和∠ACB的角平分線相交於D。

在△BDC中，

∠ABE = ∠A + ∠C

1/2∠ABE = 1/2∠A + 1/2∠C

∠1 = 1/2∠A + ∠4..............(i)

在△BDC中，

∠2 = ∠D + ∠4

∠D = ∠2 - ∠4

= ∠1 - ∠4

=(1/2∠A + ∠4) - ∠4               [由(i)]

=1/2∠A + ∠4 - ∠4

=1/2∠A

因此，∠D = 1/2∠A。

教程點

更新於: 2022年10月10日

65 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習