資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
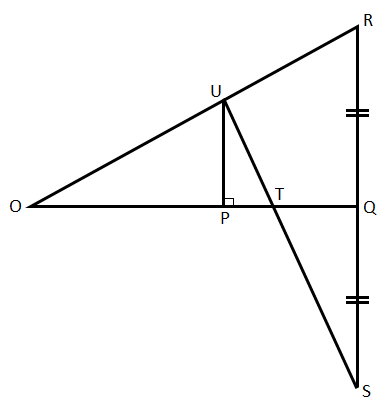
法律研究在給定圖形中，OQ 是 RS 的垂直平分線，UP 垂直於 OQ。證明 $\frac{1}{OP} \ +\ \frac{1}{OQ} \ =\ \frac{2}{OT}$。
"\n
已知：OQ 是 RS 的垂直平分線，UP 垂直於 OQ。
證明：我們需要證明 $\frac{1}{OP} \ +\ \frac{1}{OQ} \ =\ \frac{2}{OT}$。
解答
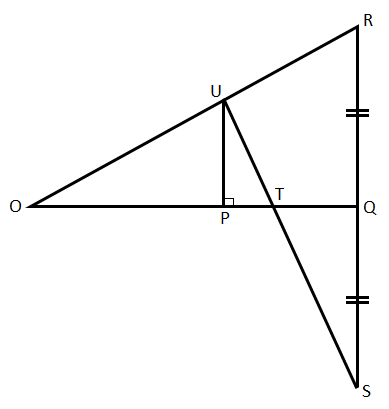
在 ∆POU 和 ∆QOR 中
- ∠O = ∠O (公共角)
- ∠P = ∠Q (均為 90o)
因此，∆POU ~ ∆QOR（根據角角相似準則）。
在兩個相似三角形中，對應邊成比例。因此，
$\frac{OP}{OQ} \ =\ \frac{PU}{QR}$ ....(i)
此外，
在 ∆UPT 和 ∆SQT 中
- ∠UTP = ∠STQ (對頂角)
- ∠P = ∠Q (均為 90o)
因此，∆UPT ~ ∆SQT（根據角角相似準則）。
在兩個相似三角形中，對應邊成比例。因此，
$\frac{PU}{QS} \ =\ \frac{PT}{QT}$
但 QS = QR，因為 Q 是 RS 的中點。所以，
$\frac{PU}{QR} \ =\ \frac{PT}{QT}$ ....(ii)
現在，由 (i) 和 (ii)
$\frac{PT}{QT}\ =\ \frac{OP}{OQ}$
$\frac{OT\ -\ OP}{OQ\ -\ OT}\ =\ \frac{OP}{OQ}$
$( OT\ -\ OP) OQ\ =\ ( OQ\ -\ OT) OP$
$OT\times OQ\ -\ OP\times OQ\ =\ OQ\times OP\ -\ OT\times OP$
$OT\times OQ\ +\ OT\times OP\ =\ OP\times OQ\ +\ OQ\times OP$
$OT( OQ\ +\ OP) \ =\ 2( OQ\ \times \ OP)$
$\frac{OQ\ +\ OP}{OQ\ \times \ OP} \ =\ \frac{2}{OT}$
$\frac{OQ}{OQ\ \times \ OP} \ +\ \frac{OP}{OQ\ \times \ OP} \ =\ \frac{2}{OT}$
$\mathbf{\frac{1}{OP} \ +\ \frac{1}{OQ} \ =\ \frac{2}{OT}}$
所以，證明了 $\frac{1}{OP} \ +\ \frac{1}{OQ} \ =\ \frac{2}{OT}$。
130 次瀏覽
