MATLAB 中最多“n”次諧波的傅立葉級數實現

---

在數學中，最多“n”次諧波的傅立葉級數是一種透過正弦和餘弦函式之和來逼近週期函式的技術。我們可以使用 MATLAB 程式設計來實現最多“n”次諧波的傅立葉級數。在討論這種實現之前，讓我們首先概述一下最多“n”次諧波的傅立葉級數。

什麼是最多“n”次諧波的傅立葉級數？

在數學中，傅立葉級數是一種將週期函式表示為正弦函式（正弦和餘弦函式）之和的方法。

最多“n”次諧波的傅立葉級數是一種將週期函式近似為正弦訊號之和的方法，其中“n”是傅立葉級數表示式中包含的諧波或項數。

從數學上講，最多“n”次諧波的傅立葉級數表示如下：

$$\mathrm{x(t) \: = \: \frac{a_{0}}{2} \: + \: \sum_{k=1}^{n}[a_{k} \cos(2\pi k\: ft)\: + \: b_{k}\sin(2\pi k\: ft)]}$$

這裡，x(t) 是給定的週期函式，f 是函式 x(t) 的基頻，$\mathrm{a_{0}}$，$\mathrm{a_{k}}$ 和 $\mathrm{b_{k}}$ 是傅立葉級數係數。

在這個表示式中，“n”表示級數中諧波或項的個數。我們可以透過增加“n”的值來向級數中新增更多諧波。

這就是關於最多“n”次諧波的傅立葉級數的基礎知識。現在讓我們討論如何在 MATLAB 中實現它。

如何在 MATLAB 中實現最多“n”次諧波的傅立葉級數

在 MATLAB 中，實現最多“n”次諧波的傅立葉級數是一個非常簡單的過程。

以下是如何在 MATLAB 中實現最多“n”次諧波的傅立葉級數的分步過程：

• 步驟 1 - 定義一個需要計算其最多“n”次諧波傅立葉級數的輸入函式。

• 步驟 2 - 計算傅立葉級數係數 $\mathrm{a_{0}}$，$\mathrm{a_{n}}$ 和 $\mathrm{b_{n}}$。

• 步驟 3 - 計算最多“n”次諧波的傅立葉級數。為此，我們可以使用迴圈機制。

• 步驟 4 - 繪製原始訊號及其傅立葉級數以進行視覺比較。

示例

讓我們透過一個示例程式來了解如何在 MATLAB 中實現最多“n”次諧波的傅立葉級數。

% MATLAB code to implement Fourier series up to "n" harmonics
% Define sample single parameters
T = 1;	% Period of the input signal
f = 1/T;	% Fundamental frequency of input signal
n = 7;	% Number of harmonics

% Create a time vector for the signal
t = 0:0.001:5*T;

% Define a function whose Fourier series is to be found
x = @(t) 0.6 + 0.4*cos(2*pi*1/T*t) + 0.2*sin(2*pi*2/T*t) + 0.3*cos(2*pi*4/T*t);

% Calculate the Fourier series coefficients
a0 = integral(@(t) x(t), 0, T) / T;
an = @(k) integral(@(t) x(t).*cos(2*pi*k*f*t), 0, T) * 2 / T;
bn = @(k) integral(@(t) x(t).*sin(2*pi*k*f*t), 0, T) * 2 / T;

% Calculate the Fourier series up to n harmonics
Fs = a0/2;
for k = 1 : n
   Fs = Fs + an(k)*cos(2*pi*k*f*t) + bn(k)*sin(2*pi*k*f*t);
end

% Plot the original signal and its Fourier series up to n harmonics
figure;
plot(t, x(t), 'r', 'LineWidth', 1, 'DisplayName', 'Original Signal');
hold on;

plot(t, Fs, 'g', 'LineWidth', 1, 'DisplayName', 'Fourier Series');

legend('Location', 'best');
xlabel('Time');
ylabel('Amplitude');

title('Fourier Series up to n Harmonics');
grid on;
hold off;

輸出

執行此程式碼時，它將生成以下繪圖：

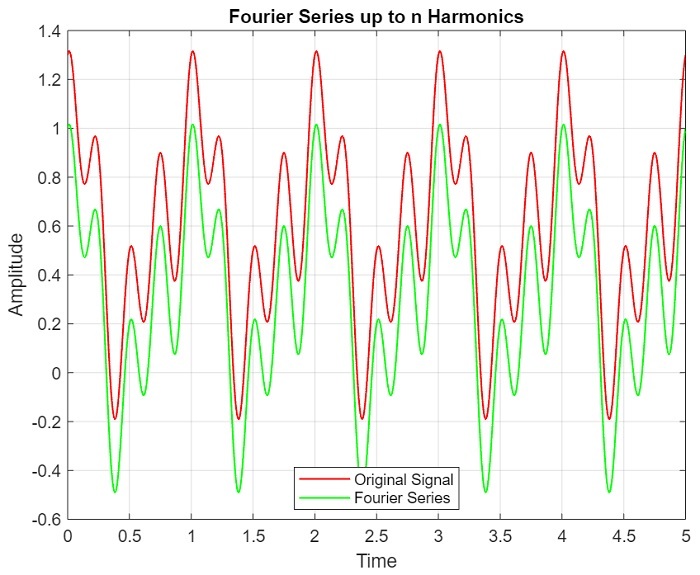
程式碼解釋

在這個例子中，我們首先定義一些訊號引數，其中“T”是輸入訊號的週期，“f”是輸入訊號的基頻，“n”是傅立葉級數計算中考慮的諧波數。

然後，我們建立一個從 0 到 5T 的時間向量來繪製訊號。

之後，我們定義一個輸入訊號“x”，其最多“n”次諧波的傅立葉級數需要計算。

接下來，我們計算傅立葉級數的係數，直流分量 $\mathrm{(a_{0})}$，餘弦項係數 $\mathrm{(a_{n})}$ 和正弦項係數 $\mathrm{(b_{n})}$。

然後，我們用直流分量初始化傅立葉級數“Fs”。之後，我們定義一個迴圈，將傅立葉級數的項新增到每個諧波，直到“n”計算輸入訊號的傅立葉級數。

最後，我們繪製輸入訊號及其最多“n”次諧波的傅立葉級數。

結論

總之，最多“n”次諧波的傅立葉級數是一種將週期訊號表示為具有“n”項的正弦和餘弦函式之和的方法。我們可以使用 MATLAB 程式設計來計算函式最多“n”次諧波的傅立葉級數。

在本教程中，我解釋了在 MATLAB 中實現最多“n”次諧波的傅立葉級數中涉及的步驟以及一個示例程式。示例程式實際上演示了計算週期函式最多“n”次諧波的傅立葉級數的過程。