模糊邏輯 - 集合論

---

---

模糊集可以被認為是經典集合的擴充套件和極度簡化。它最好在集合成員關係的背景下理解。基本上，它允許部分成員關係，這意味著它包含在集合中具有不同程度成員關係的元素。由此，我們可以理解經典集合和模糊集之間的區別。經典集合包含滿足精確成員屬性的元素，而模糊集包含滿足不精確成員屬性的元素。

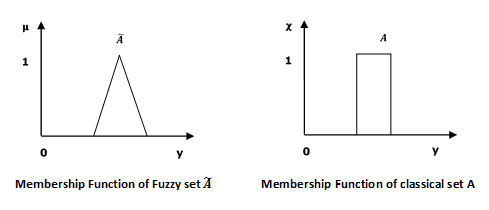
數學概念

資訊宇宙 U 中的模糊集$\widetilde{A}$可以定義為一組有序對，可以用數學表示為：

$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$

這裡$\mu _{\widetilde{A}}\left ( y \right )$ = y 在 $\widetilde{A}$ 中的隸屬度，取值範圍為 0 到 1，即 $\mu _{\widetilde{A}}(y)\in \left [ 0,1 \right ]$。

模糊集的表示

現在讓我們考慮資訊宇宙的兩種情況，並瞭解如何表示模糊集。

情況 1

當資訊宇宙 U 是離散且有限時：

$$\widetilde{A} = \left \{ \frac{\mu _{\widetilde{A}}\left ( y_1 \right )}{y_1} +\frac{\mu _{\widetilde{A}}\left ( y_2 \right )}{y_2} +\frac{\mu _{\widetilde{A}}\left ( y_3 \right )}{y_3} +...\right \}$$

$= \left \{ \sum_{i=1}^{n}\frac{\mu _{\widetilde{A}}\left ( y_i \right )}{y_i} \right \}$

情況 2

當資訊宇宙 U 是連續且無限時：

$$\widetilde{A} = \left \{ \int \frac{\mu _{\widetilde{A}}\left ( y \right )}{y} \right \}$$

在上述表示中，求和符號表示每個元素的集合。

模糊集的運算

對於兩個模糊集 $\widetilde{A}$ 和 $\widetilde{B}$，資訊宇宙 U 和宇宙中的一個元素 y，以下關係表示模糊集上的並集、交集和補集運算。

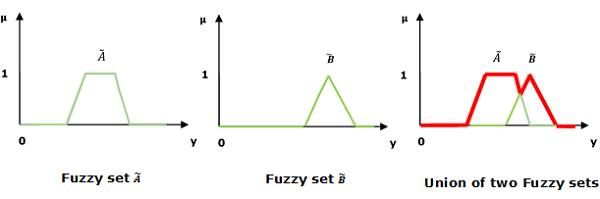
並集/模糊“或”

讓我們考慮以下表示來理解並集/模糊“或”關係是如何工作的：

$$\mu _{{\widetilde{A}\cup \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\vee \mu _\widetilde{B} \quad \forall y \in U$$

這裡 ∨ 表示“max”運算。

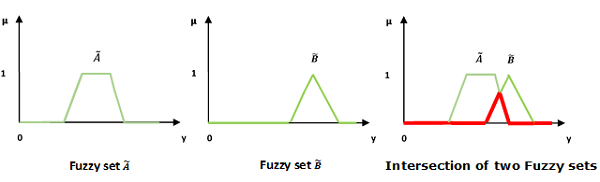
交集/模糊“與”

讓我們考慮以下表示來理解交集/模糊“與”關係是如何工作的：

$$\mu _{{\widetilde{A}\cap \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\wedge \mu _\widetilde{B} \quad \forall y \in U$$

這裡 ∧ 表示“min”運算。

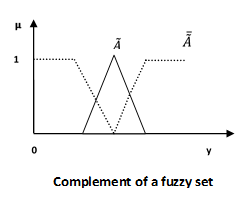
補集/模糊“非”

讓我們考慮以下表示來理解補集/模糊“非”關係是如何工作的：

$$\mu _{\widetilde{A}} = 1-\mu _{\widetilde{A}}\left ( y \right )\quad y \in U$$

模糊集的性質

讓我們討論模糊集的不同性質。

交換律

對於兩個模糊集 $\widetilde{A}$ 和 $\widetilde{B}$，此性質指出：

$$\widetilde{A}\cup \widetilde{B} = \widetilde{B}\cup \widetilde{A}$$

$$\widetilde{A}\cap \widetilde{B} = \widetilde{B}\cap \widetilde{A}$$

結合律

對於三個模糊集 $\widetilde{A}$，$\widetilde{B}$ 和 $\widetilde{C}$，此性質指出：

$$(\widetilde{A}\cup \left \widetilde{B}) \cup \widetilde{C} \right = \left \widetilde{A} \cup (\widetilde{B}\right )\cup \widetilde{C})$$

$$(\widetilde{A}\cap \left \widetilde{B}) \cap \widetilde{C} \right = \left \widetilde{A} \cup (\widetilde{B}\right \cap \widetilde{C})$$

分配律

對於三個模糊集 $\widetilde{A}$，$\widetilde{B}$ 和 $\widetilde{C}$，此性質指出：

$$\widetilde{A}\cup \left ( \widetilde{B} \cap \widetilde{C}\right ) = \left ( \widetilde{A} \cup \widetilde{B}\right )\cap \left ( \widetilde{A}\cup \widetilde{C} \right )$$

$$\widetilde{A}\cap \left ( \widetilde{B}\cup \widetilde{C} \right ) = \left ( \widetilde{A} \cap \widetilde{B} \right )\cup \left ( \widetilde{A}\cap \widetilde{C} \right )$$

冪等律

對於任何模糊集 $\widetilde{A}$，此性質指出：

$$\widetilde{A}\cup \widetilde{A} = \widetilde{A}$$

$$\widetilde{A}\cap \widetilde{A} = \widetilde{A}$$

恆等律

對於模糊集 $\widetilde{A}$ 和全集 U，此性質指出：

$$\widetilde{A}\cup \varphi = \widetilde{A}$$

$$\widetilde{A}\cap U = \widetilde{A}$$

$$\widetilde{A}\cap \varphi = \varphi$$

$$\widetilde{A}\cup U = U$$

傳遞律

對於三個模糊集 $\widetilde{A}$，$\widetilde{B}$ 和 $\widetilde{C}$，此性質指出：

$$如果 \: \widetilde{A}\subseteq \widetilde{B}\subseteq \widetilde{C},\:則\:\widetilde{A}\subseteq \widetilde{C}$$

對合律

對於任何模糊集 $\widetilde{A}$，此性質指出：

$$\overline{\overline{\widetilde{A}}} = \widetilde{A}$$

德摩根定律

該定律在證明重言式和矛盾方面起著至關重要的作用。該定律指出：

$$\overline{{\widetilde{A}\cap \widetilde{B}}} = \overline{\widetilde{A}}\cup \overline{\widetilde{B}}$$

$$\overline{{\widetilde{A}\cup \widetilde{B}}} = \overline{\widetilde{A}}\cap \overline{\widetilde{B}}$$