模糊邏輯 - 會員函式

---

---

我們已經知道，模糊邏輯不是模糊的邏輯，而是用來描述模糊性的邏輯。這種模糊性最顯著的特徵就是它的隸屬函式。換句話說，我們可以說隸屬函式代表了模糊邏輯中的真值程度。

以下是一些與隸屬函式相關的要點：

• 隸屬函式最初由 Lotfi A. Zadeh 於 1965 年在其第一篇研究論文“模糊集”中提出。

• 隸屬函式刻畫了模糊性（即模糊集中所有資訊），無論模糊集中的元素是離散的還是連續的。

• 隸屬函式可以定義為一種透過經驗而非知識來解決實際問題的技術。

• 隸屬函式以圖形形式表示。

• 定義模糊性的規則本身也是模糊的。

數學表示法

我們已經學習過，在資訊宇宙 U 中的模糊集 Ã 可以定義為有序對的集合，可以用數學方式表示為：

$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$

這裡 $\mu \widetilde{A}\left (\bullet \right )$ = $\widetilde{A}$ 的隸屬函式；它取值範圍為 0 到 1，即 $\mu \widetilde{A}\left (\bullet \right )\in \left [ 0,1 \right ]$。隸屬函式 $\mu \widetilde{A}\left (\bullet \right )$ 將 U 對映到隸屬空間 M。

上述隸屬函式中的點 $\left (\bullet \right )$ 代表模糊集中的元素；無論是離散的還是連續的。

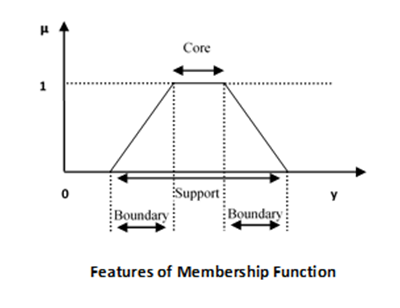
隸屬函式的特徵

現在我們將討論隸屬函式的不同特徵。

核心

對於任何模糊集 $\widetilde{A}$，隸屬函式的核心是宇宙中以完全隸屬於該集合為特徵的區域。因此，核心由資訊宇宙中所有滿足以下條件的元素 y 組成：

$$\mu _{\widetilde{A}}\left ( y \right ) = 1$$

支撐

對於任何模糊集 $\widetilde{A}$，隸屬函式的支撐是宇宙中以非零隸屬於該集合為特徵的區域。因此，核心由資訊宇宙中所有滿足以下條件的元素 y 組成：

$$\mu _{\widetilde{A}}\left ( y \right ) > 0$$

邊界

對於任何模糊集 $\widetilde{A}$，隸屬函式的邊界是宇宙中以非零但非完全隸屬於該集合為特徵的區域。因此，核心由資訊宇宙中所有滿足以下條件的元素 y 組成：

$$1 > \mu _{\widetilde{A}}\left ( y \right ) > 0$$

模糊化

可以定義為將清晰集轉換為模糊集或將模糊集轉換為更模糊集的過程。基本上，此操作將精確的清晰輸入值轉換為語言變數。

以下是兩種重要的模糊化方法：

支撐模糊化（s-模糊化）方法

在這種方法中，模糊化後的集合可以用以下關係表示：

$$\widetilde{A} = \mu _1Q\left ( x_1 \right )+\mu _2Q\left ( x_2 \right )+...+\mu _nQ\left ( x_n \right )$$

這裡模糊集 $Q\left ( x_i \right )$ 被稱為模糊化的核。這種方法是透過保持 $\mu _i$ 常數並將其轉換為模糊集 $Q\left ( x_i \right )$ 來實現的。

等級模糊化（g-模糊化）方法

它與上述方法非常相似，但主要區別在於它保持 $x_i$ 常數，並將 $\mu _i$ 表示為模糊集。

去模糊化

可以定義為將模糊集簡化為清晰集或將模糊成員轉換為清晰成員的過程。

我們已經學習過，模糊化過程涉及從清晰量到模糊量的轉換。在許多工程應用中，需要對結果或更確切地說是“模糊結果”進行去模糊化，以便將其轉換為清晰結果。從數學上講，去模糊化過程也稱為“四捨五入”。

下面描述了不同的去模糊化方法：

最大隸屬度法

此方法僅限於峰值輸出函式，也稱為高度法。從數學上講，它可以表示為：

$$\mu _{\widetilde{A}}\left ( x^* \right )>\mu _{\widetilde{A}}\left ( x \right ) \: for \:all\:x \in X$$

這裡，$x^*$ 是去模糊化的輸出。

質心法

此方法也稱為面積中心法或重心法。從數學上講，去模糊化的輸出 $x^*$ 將表示為：

$$x^* = \frac{\int \mu _{\widetilde{A}}\left ( x \right ).xdx}{\int \mu _{\widetilde{A}}\left ( x \right ).dx}$$

加權平均法

在這種方法中，每個隸屬函式都以其最大隸屬度值加權。從數學上講，去模糊化的輸出 $x^*$ 將表示為：

$$x^* = \frac{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right ).\overline{x_i}}{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right )}$$

均值最大隸屬度

此方法也稱為最大值的中點。從數學上講，去模糊化的輸出 $x^*$ 將表示為：

$$x^* = \frac{\displaystyle \sum_{i=1}^{n}\overline{x_i}}{n}$$