模糊邏輯 - 快速指南

模糊邏輯 - 簡介

單詞模糊指的是不明確或含糊的事物。任何持續變化的事件、過程或函式都不能總是被定義為真或假，這意味著我們需要以模糊的方式來定義此類活動。

什麼是模糊邏輯？

模糊邏輯類似於人類的決策方法。它處理模糊和不精確的資訊。這是對現實世界問題的極大簡化，基於真值的程度，而不是像布林邏輯那樣的通常的真/假或1/0。

請看下圖。它顯示在模糊系統中，值由0到1範圍內的數字表示。其中1.0表示絕對真，0.0表示絕對假。表示模糊系統中值的數字稱為真值。

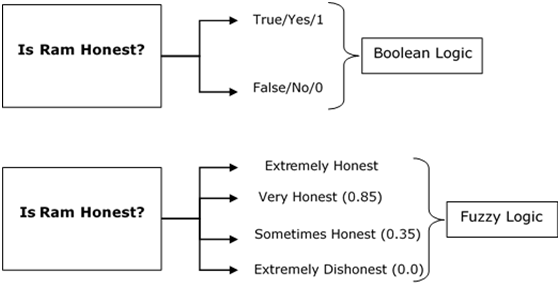
換句話說，我們可以說模糊邏輯不是模糊的邏輯，而是用於描述模糊性的邏輯。我們可以用許多其他例子來理解模糊邏輯的概念。

模糊邏輯由Lotfi A. Zadeh於1965年在他的研究論文“模糊集”中提出。他被認為是模糊邏輯之父。

模糊邏輯 - 經典集合論

集合是不同元素的無序集合。可以使用集合括號列出其元素來明確地寫出它。如果元素的順序改變或集合的任何元素重複，則不會對集合進行任何更改。

例子

所有正整數的集合。
太陽系中所有行星的集合。
印度所有邦的集合。
字母表中所有小寫字母的集合。

集合的數學表示

集合可以用兩種方式表示：

列舉法或表格法

在這種形式中，集合透過列出構成它的所有元素來表示。元素用大括號括起來，並用逗號分隔。

以下是列舉法或表格法中集合的例子：

英語字母表中的母音集合，A = {a,e,i,o,u}
小於10的奇數集合，B = {1,3,5,7,9}

集合構造法

在這種形式中，集合是透過指定集合元素共有的屬性來定義的。集合被描述為A = {x:p(x)}

示例1 - 集合{a,e,i,o,u}寫成

A = {x:x是英語字母表中的母音}

示例2 - 集合{1,3,5,7,9}寫成

B = {x:1 ≤ x < 10 且 (x%2) ≠ 0}

如果元素x是任何集合S的成員，則表示為x∈S；如果元素y不是集合S的成員，則表示為y∉S。

示例 - 如果S = {1,1.2,1.7,2}，則1 ∈ S，但1.5 ∉ S

集合的基數

集合S的基數，記為|S|，是集合的元素個數。這個數也稱為基數。如果一個集合有無限多個元素，則它的基數是∞。

示例 - |{1,4,3,5}| = 4，|{1,2,3,4,5,…}| = ∞

如果有兩個集合X和Y，|X| = |Y|表示兩個集合X和Y具有相同的基數。當X中的元素個數正好等於Y中的元素個數時，就會發生這種情況。在這種情況下，存在從X到Y的雙射函式'f'。

|X| ≤ |Y|表示集合X的基數小於或等於集合Y的基數。當X中的元素個數小於或等於Y中的元素個數時，就會發生這種情況。這裡，存在從X到Y的單射函式'f'。

|X| < |Y|表示集合X的基數小於集合Y的基數。當X中的元素個數小於Y中的元素個數時，就會發生這種情況。這裡，從X到Y的函式'f'是單射函式，但不是雙射函式。

如果|X| ≤ |Y|並且|X| ≥ |Y|，則|X| = |Y|。集合X和Y通常稱為等價集合。

集合的型別

集合可以分為許多型別；其中一些是有限集、無限集、子集、全集、真子集、單元素集等。

有限集

包含一定數量元素的集合稱為有限集。

示例 - S = {x|x ∈ N 且 70 > x > 50}

無限集

包含無限多個元素的集合稱為無限集。

示例 - S = {x|x ∈ N 且 x > 10}

子集

如果集合X的每個元素都是集合Y的元素，則集合X是集合Y的子集（寫成X ⊆ Y）。

示例1 - 令X = {1,2,3,4,5,6}且Y = {1,2}。這裡集合Y是集合X的子集，因為集合Y的所有元素都在集合X中。因此，我們可以寫成Y⊆X。

示例2 - 令X = {1,2,3}且Y = {1,2,3}。這裡集合Y是集合X的子集（而不是真子集），因為集合Y的所有元素都在集合X中。因此，我們可以寫成Y⊆X。

真子集

術語“真子集”可以定義為“是子集，但不等於”。如果集合X的每個元素都是集合Y的元素，並且|X| < |Y|，則集合X是集合Y的真子集（寫成X ⊂ Y）。

示例 - 令X = {1,2,3,4,5,6}且Y = {1,2}。這裡集合Y ⊂ X，因為Y中的所有元素也包含在X中，並且X至少有一個比集合Y多的元素。

全集

它是特定上下文或應用程式中所有元素的集合。該上下文或應用程式中的所有集合本質上都是這個全集的子集。全集表示為U。

示例 - 我們可以將U定義為地球上所有動物的集合。在這種情況下，所有哺乳動物的集合是U的子集，所有魚類的集合是U的子集，所有昆蟲的集合是U的子集，等等。

空集或null集

空集不包含任何元素。它用Φ表示。由於空集中的元素數量是有限的，因此空集是有限集。空集或null集的基數為零。

示例 – S = {x|x ∈ N 且 7 < x < 8} = Φ

單元素集或單元集

單元素集或單元集只包含一個元素。單元素集表示為{s}。

示例 - S = {x|x ∈ N，7 < x < 9} = {8}

相等集合

如果兩個集合包含相同的元素，則它們被稱為相等。

示例 - 如果A = {1,2,6}且B = {6,1,2}，則它們相等，因為集合A的每個元素都是集合B的元素，並且集合B的每個元素都是集合A的元素。

等價集合

如果兩個集合的基數相同，則它們被稱為等價集合。

示例 - 如果A = {1,2,6}且B = {16,17,22}，則它們是等價的，因為A的基數等於B的基數。即|A| = |B| = 3

重疊集合

至少有一個公共元素的兩個集合稱為重疊集合。對於重疊集合：

$$n\left ( A\cup B \right ) = n\left ( A \right ) + n\left ( B \right ) - n\left ( A\cap B \right )$$

$$n\left ( A\cup B \right ) = n\left ( A-B \right )+n\left ( B-A \right )+n\left ( A\cap B \right )$$

$$n\left ( A \right ) = n\left ( A-B \right )+n\left ( A\cap B \right )$$

$$n\left ( B \right ) = n\left ( B-A \right )+n\left ( A\cap B \right )$$

示例 - 令A = {1,2,6}且B = {6,12,42}。有一個公共元素'6'，因此這些集合是重疊集合。

不相交集合

如果兩個集合A和B沒有任何公共元素，則它們被稱為不相交集合。因此，不相交集合具有以下性質：

$$n\left ( A\cap B \right ) = \phi$$

$$n\left ( A\cup B \right ) = n\left ( A \right )+n\left ( B \right )$$

示例 - 令A = {1,2,6}且B = {7,9,14}，沒有一個公共元素，因此這些集合是重疊集合。(此處應為不相交集合)

經典集合上的運算

集合運算包括集合並、集合交、集合差、集合補和笛卡爾積。

並集

集合A和B的並集（記作A ∪ B）是屬於A、屬於B或同時屬於A和B的元素的集合。因此，A ∪ B = {x|x ∈ A 或 x ∈ B}。

示例 - 如果A = {10,11,12,13}且B = {13,14,15}，則A ∪ B = {10,11,12,13,14,15} - 公共元素只出現一次。

交集

集合A和B的交集（記作A ∩ B）是同時屬於A和B的元素的集合。因此，A ∩ B = {x|x ∈ A 且 x ∈ B}。

差集/相對補集

集合A和B的差集（記作A–B）是隻屬於A而不屬於B的元素的集合。因此，A − B = {x|x ∈ A 且 x ∉ B}。

示例 - 如果A = {10,11,12,13}且B = {13,14,15}，則(A − B) = {10,11,12}且(B − A) = {14,15}。在這裡，我們可以看到(A − B) ≠ (B − A)

集合的補集

集合A的補集（記作A′）是不屬於集合A的元素的集合。因此，A′ = {x|x ∉ A}。

更具體地說，A′ = (U−A)，其中U是包含所有物件的全集。

示例 - 如果A = {x|x屬於奇整數集合}，則A′ = {y|y不屬於奇整數集合}

笛卡爾積/交叉積

n個集合A1,A2,…An的笛卡爾積，記作A1 × A2...× An，可以定義為所有可能的序對(x1,x2,…xn)，其中x1 ∈ A1,x2 ∈ A2,…xn ∈ An

示例 - 如果我們取兩個集合A = {a,b}和B = {1,2}，

A和B的笛卡爾積寫成：A × B = {(a,1),(a,2),(b,1),(b,2)}

B與A的笛卡爾積寫成− B × A = {(1,a),(1,b),(2,a),(2,b)}

經典集合的性質

集合的性質在獲得解的過程中起著重要作用。以下是經典集合的不同性質：

交換律

對於兩個集合A和B，該性質指出：

$$A \cup B = B \cup A$$

$$A \cap B = B \cap A$$

結合律

對於三個集合A、B和C，該性質指出：

$$A\cup \left ( B\cup C \right ) = \left ( A\cup B \right )\cup C$$

$$A\cap \left ( B\cap C \right ) = \left ( A\cap B \right )\cap C$$

分配律

對於三個集合A、B和C，該性質指出：

$$A\cup \left ( B\cap C \right ) = \left ( A\cup B \right )\cap \left ( A\cup C \right )$$

$$A\cap \left ( B\cup C \right ) = \left ( A\cap B \right )\cup \left ( A\cap C \right )$$

冪等律

對於任何集合A，該性質指出：

$$A\cup A = A$$

$$A\cap A = A$$

恆等律

對於集合A和全集X，該性質指出：

$$A\cup \varphi = A$$

$$A\cap X = A$$

$$A\cap \varphi = \varphi$$

$$A\cup X = X$$

傳遞律

對於三個集合A、B和C，該性質指出：

如果 $A\subseteq B\subseteq C$，則 $A\subseteq C$

對合律

對於任何集合A，該性質指出：

$$\overline{{\overline{A}}} = A$$

德摩根律

這是一個非常重要的定律，它有助於證明重言式和矛盾。該定律指出：

$$\overline{A\cap B} = \overline{A} \cup \overline{B}$$

$$\overline{A\cup B} = \overline{A} \cap \overline{B}$$

模糊邏輯 - 集合論

模糊集可以被認為是經典集合的擴充套件和粗略簡化。它最好在集合成員資格的背景下理解。基本上，它允許部分成員資格，這意味著它包含具有不同成員資格程度的元素。由此，我們可以理解經典集合和模糊集之間的區別。經典集合包含滿足精確成員資格屬性的元素，而模糊集包含滿足不精確成員資格屬性的元素。

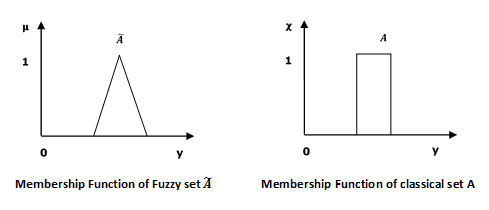
數學概念

資訊宇宙U中的模糊集$\widetilde{A}$可以定義為一組有序對，可以用數學表示為：

$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$

這裡$\mu _{\widetilde{A}}\left ( y \right )$ = y在$\widetilde{A}$中的隸屬度，取值範圍為0到1，即$\mu _{\widetilde{A}}(y)\in \left [ 0,1 \right ]$。

模糊集的表示

現在讓我們考慮資訊宇宙的兩種情況，並瞭解如何表示模糊集。

情況1

當資訊宇宙U是離散且有限的：

$$\widetilde{A} = \left \{ \frac{\mu _{\widetilde{A}}\left ( y_1 \right )}{y_1} +\frac{\mu _{\widetilde{A}}\left ( y_2 \right )}{y_2} +\frac{\mu _{\widetilde{A}}\left ( y_3 \right )}{y_3} +...\right \}$$

$= \left \{ \sum_{i=1}^{n}\frac{\mu _{\widetilde{A}}\left ( y_i \right )}{y_i} \right \}$

情況2

當資訊宇宙U是連續且無限的：

$$\widetilde{A} = \left \{ \int \frac{\mu _{\widetilde{A}}\left ( y \right )}{y} \right \}$$

在上述表示中，求和符號代表每個元素的集合。

模糊集上的運算

對於兩個模糊集$\widetilde{A}$和$\widetilde{B}$，資訊宇宙U和宇宙中的一個元素y，以下關係表示模糊集上的並、交和補運算。

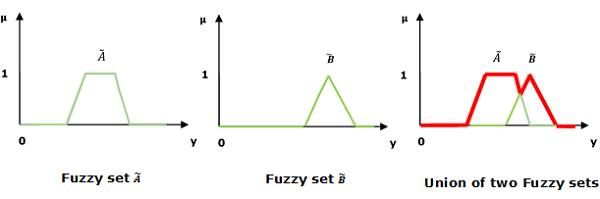
並/模糊“或”

讓我們考慮以下表示來理解並/模糊“或”關係是如何工作的：

$$\mu _{{\widetilde{A}\cup \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\vee \mu _\widetilde{B} \quad \forall y \in U$$

這裡∨代表“最大”運算。

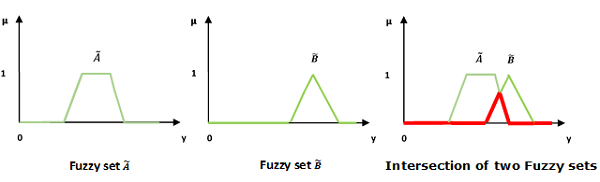
交/模糊“與”

讓我們考慮以下表示來理解交/模糊“與”關係是如何工作的：

$$\mu _{{\widetilde{A}\cap \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\wedge \mu _\widetilde{B} \quad \forall y \in U$$

這裡∧代表“最小”運算。

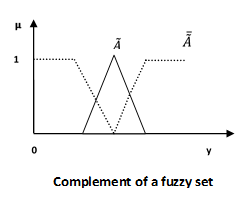
補/模糊“非”

讓我們考慮以下表示來理解補/模糊“非”關係是如何工作的：

$$\mu _{\widetilde{A}} = 1-\mu _{\widetilde{A}}\left ( y \right )\quad y \in U$$

模糊集的性質

讓我們討論模糊集的不同性質。

交換律

對於兩個模糊集$\widetilde{A}$和$\widetilde{B}$，該性質指出：

$$\widetilde{A}\cup \widetilde{B} = \widetilde{B}\cup \widetilde{A}$$

$$\widetilde{A}\cap \widetilde{B} = \widetilde{B}\cap \widetilde{A}$$

結合律

對於三個模糊集$\widetilde{A}$、$\widetilde{B}$和$\widetilde{C}$，該性質指出：

$$(\widetilde{A}\cup \widetilde{B}) \cup \widetilde{C} = \widetilde{A} \cup (\widetilde{B}\cup \widetilde{C})$$

$$(\widetilde{A}\cap \widetilde{B}) \cap \widetilde{C} = \widetilde{A} \cap (\widetilde{B}\cap \widetilde{C})$$

分配律

對於三個模糊集$\widetilde{A}$、$\widetilde{B}$和$\widetilde{C}$，該性質指出：

$$\widetilde{A}\cup \left ( \widetilde{B} \cap \widetilde{C}\right ) = \left ( \widetilde{A} \cup \widetilde{B}\right )\cap \left ( \widetilde{A}\cup \widetilde{C} \right )$$

$$\widetilde{A}\cap \left ( \widetilde{B}\cup \widetilde{C} \right ) = \left ( \widetilde{A} \cap \widetilde{B} \right )\cup \left ( \widetilde{A}\cap \widetilde{C} \right )$$

冪等律

對於任何模糊集$\widetilde{A}$，該性質指出：

$$\widetilde{A}\cup \widetilde{A} = \widetilde{A}$$

$$\widetilde{A}\cap \widetilde{A} = \widetilde{A}$$

恆等律

對於模糊集$\widetilde{A}$和全集U，該性質指出：

$$\widetilde{A}\cup \varphi = \widetilde{A}$$

$$\widetilde{A}\cap U = \widetilde{A}$$

$$\widetilde{A}\cap \varphi = \varphi$$

$$\widetilde{A}\cup U = U$$

傳遞律

對於三個模糊集$\widetilde{A}$、$\widetilde{B}$和$\widetilde{C}$，該性質指出：

$$如果 \: \widetilde{A}\subseteq \widetilde{B}\subseteq \widetilde{C},\:則\:\widetilde{A}\subseteq \widetilde{C}$$

對合律

對於任何模糊集$\widetilde{A}$，該性質指出：

$$\overline{\overline{\widetilde{A}}} = \widetilde{A}$$

德摩根律

該定律在證明重言式和矛盾中起著至關重要的作用。該定律指出：

$$\overline{{\widetilde{A}\cap \widetilde{B}}} = \overline{\widetilde{A}}\cup \overline{\widetilde{B}}$$

$$\overline{{\widetilde{A}\cup \widetilde{B}}} = \overline{\widetilde{A}}\cap \overline{\widetilde{B}}$$

模糊邏輯 -隸屬函式

我們已經知道，模糊邏輯不是模糊的邏輯，而是用於描述模糊性的邏輯。這種模糊性最好用其隸屬函式來表徵。換句話說，我們可以說隸屬函式表示模糊邏輯中的真值程度。

以下是關於隸屬函式的一些要點：

隸屬函式最早由Lotfi A. Zadeh於1965年在其第一篇研究論文“模糊集”中提出。
隸屬函式表徵模糊性（即模糊集中的所有資訊），無論模糊集中的元素是離散的還是連續的。
隸屬函式可以定義為透過經驗而不是知識來解決實際問題的技術。
隸屬函式以圖形形式表示。
定義模糊性的規則也是模糊的。

數學符號

我們已經學習過，資訊宇宙U中的模糊集$\widetilde{A}$可以定義為一組有序對，可以用數學表示為：

$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$

這裡$\mu_{\widetilde{A}}(\bullet)$ = $\widetilde{A}$的隸屬函式；其取值範圍為0到1，即$\mu_{\widetilde{A}}(\bullet) \in [0, 1]$。隸屬函式$\mu_{\widetilde{A}}(\bullet)$ 將U對映到隸屬空間M。

上述隸屬函式中的點$(\bullet)$表示模糊集中的元素；無論是離散的還是連續的。

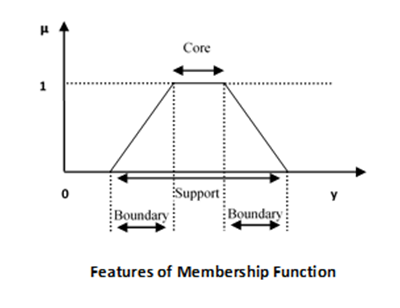
隸屬函式的特徵

我們現在將討論隸屬函式的不同特徵。

核

對於任何模糊集$\widetilde{A}$，隸屬函式的核是宇宙中以完全隸屬於集合為特徵的區域。因此，核由資訊宇宙的所有那些元素y組成，使得：

$$\mu _{\widetilde{A}}\left ( y \right ) = 1$$

支集

對於任何模糊集$\widetilde{A}$，隸屬函式的支集是宇宙中以非零隸屬於集合為特徵的區域。因此，核由資訊宇宙的所有那些元素y組成，使得：

$$\mu _{\widetilde{A}}\left ( y \right ) > 0$$

邊界

對於任何模糊集$\widetilde{A}$，隸屬函式的邊界是宇宙中以非零但非完全隸屬於集合為特徵的區域。因此，核由資訊宇宙的所有那些元素y組成，使得：

$$1 > \mu _{\widetilde{A}}\left ( y \right ) > 0$$

模糊化

它可以定義為將清晰集轉換為模糊集或將模糊集轉換為更模糊集的過程。基本上，此操作將精確的清晰輸入值轉換為語言變數。

以下是兩種重要的模糊化方法：

支集模糊化(s-模糊化)方法

在這種方法中，模糊集可以用以下關係表示：

$$\widetilde{A} = \mu _1Q\left ( x_1 \right )+\mu _2Q\left ( x_2 \right )+...+\mu _nQ\left ( x_n \right )$$

這裡模糊集$Q\left ( x_i \right )$被稱為模糊化的核。該方法透過保持$\mu _i$不變，並將$x_i$轉換為模糊集$Q\left ( x_i \right )$來實現。

等級模糊化(g-模糊化)方法

它與上述方法非常相似，但主要區別在於它保持$x_i$不變，並將$\mu _i$表示為模糊集。

去模糊化

它可以定義為將模糊集簡化為清晰集或將模糊成員轉換為清晰成員的過程。

我們已經學習過，模糊化過程涉及從清晰量到模糊量的轉換。在許多工程應用中，需要對結果或“模糊結果”進行去模糊化，以便將其轉換為清晰結果。在數學上，去模糊化過程也稱為“四捨五入”。

下面描述了不同的去模糊化方法：

最大隸屬度法

該方法僅限於峰值輸出函式，也稱為高度法。在數學上，它可以表示如下：

$$\mu _{\widetilde{A}}\left ( x^* \right )>\mu _{\widetilde{A}}\left ( x \right ) \: 對所有 \:x \in X$$

這裡，$x^*$是去模糊化後的輸出。

質心法

該方法也稱為面積中心法或重心法。在數學上，去模糊化後的輸出$x^*$將表示為：

$$x^* = \frac{\int \mu _{\widetilde{A}}\left ( x \right ).xdx}{\int \mu _{\widetilde{A}}\left ( x \right ).dx}$$

加權平均法

在這種方法中，每個隸屬函式都按其最大隸屬度加權。在數學上，去模糊化後的輸出$x^*$將表示為：

$$x^* = \frac{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right ).\overline{x_i}}{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right )}$$

平均最大隸屬度法

該方法也稱為最大值的中點法。在數學上，去模糊化後的輸出$x^*$將表示為：

$$x^* = \frac{\displaystyle \sum_{i=1}^{n}\overline{x_i}}{n}$$

模糊邏輯 - 傳統模糊知識回顧

邏輯最初只是研究區分可靠論證和不可靠論證的學科，如今已發展成為一個強大而嚴謹的體系，可以透過已知為真的其他陳述來發現真實的陳述。

謂詞邏輯

這種邏輯處理謂詞，謂詞是包含變數的命題。

謂詞是在某個特定域上定義的一個或多個變數的表示式。透過為變數賦值或對變數進行量化，可以將包含變數的謂詞變成命題。

以下是一些謂詞示例：

令 E(x, y) 表示 "x = y"
令 X(a, b, c) 表示 "a + b + c = 0"
令 M(x, y) 表示 "x 與 y 結婚"

命題邏輯

命題是由宣告性語句組成的集合，這些語句具有真值“真”或真值“假”。命題由命題變數和連線片語成。命題變數用大寫字母（A、B 等）表示。連線詞連線命題變數。

以下是一些命題示例：

"人是凡人"，其真值為“真”
"12 + 9 = 3 – 2"，其真值為“假”

以下不是命題：

"A 小於 2" − 因為除非我們給 A 一個特定的值，否則我們無法判斷該陳述是真還是假。

連線詞

在命題邏輯中，我們使用以下五個連線詞：

或 (∨)
與 (∧)
非/否定 (¬)
蘊涵/如果-那麼 (→)
當且僅當 (⇔)

或 (∨)

兩個命題 A 和 B 的或運算（寫成 A∨B）如果命題變數 A 或 B 中至少有一個為真，則結果為真。

真值表如下：

A	B	A ∨ B
真	真	真
真	假	真
假	真	真
假	假	假

與 (∧)

兩個命題 A 和 B 的與運算（寫成 A∧B）如果命題變數 A 和 B 都為真，則結果為真。

真值表如下：

A	B	A ∧ B
真	真	真
真	假	假
假	真	假
假	假	假

否定 (¬)

命題 A 的否定（寫成 ¬A）當 A 為真時為假，當 A 為假時為真。

真值表如下：

A	¬A
真	假
假	真

蘊涵/如果-那麼 (→)

蘊涵 A→B 是命題“如果 A，那麼 B”。如果 A 為真而 B 為假，則結果為假。其餘情況為真。

真值表如下：

A	B	A→B
真	真	真
真	假	假
假	真	真
假	假	真

當且僅當 (⇔)

A⇔B 是一個雙條件邏輯連線詞，當 p 和 q 相同（即兩者都為假或兩者都為真）時為真。

真值表如下：

A	B	A⇔B
真	真	真
真	假	假
假	真	假
假	假	真

良構公式

良構公式 (wff) 是滿足以下條件之一的謂詞：

所有命題常量和命題變數都是良構公式。
如果 x 是一個變數，而 Y 是一個良構公式，則 ∀xY 和 ∃xY 也是良構公式。
真值和假值是良構公式。
每個原子公式都是良構公式。
所有連線良構公式的連線詞都是良構公式。

量詞

謂詞的變數由量詞量化。謂詞邏輯中有兩種型別的量詞：

全稱量詞
存在量詞

全稱量詞

全稱量詞指出其範圍內的語句對於特定變數的每個值都為真。它用符號 ∀ 表示。

∀xP(x) 讀作對於 x 的每個值，P(x) 都為真。

示例 − “人是凡人”可以轉換為命題形式 ∀xP(x)。這裡，P(x) 是表示 x 是凡人的謂詞，論域是所有的人。

存在量詞

存在量詞指出其範圍內的語句對於特定變數的某些值都為真。它用符號 ∃ 表示。

∃xP(x) 讀作對於 x 的某些值，P(x) 為真。

示例 − “有些人是不誠實的”可以轉換為命題形式 ∃x P(x)，其中 P(x) 是表示 x 不誠實的謂詞，論域是某些人。

巢狀量詞

如果我們使用的量詞出現在另一個量詞的範圍內，則稱為巢狀量詞。

例子

∀ a∃bP(x,y)，其中 P(a,b) 表示 a+b = 0
∀ a∀b∀cP(a,b,c)，其中 P(a,b) 表示 a+(b+c) = (a+b)+c

注意 − ∀a∃bP(x,y) ≠ ∃a∀bP(x,y)

模糊邏輯 - 近似推理

以下是近似推理的不同模式：

範疇推理

在這種近似推理模式中，假設不包含模糊量詞和模糊機率的前件採用規範形式。

定性推理

在這種近似推理模式中，前件和後件具有模糊語言變數；系統的輸入-輸出關係表示為模糊 IF-THEN 規則的集合。這種推理主要用於控制系統分析。

三段論推理

在這種近似推理模式中，包含模糊量詞的前件與推理規則相關。它表示為：

x = S₁A 是 B

y = S₂C 是 D

------------------------

z = S₃E 是 F

這裡 A、B、C、D、E、F 是模糊謂詞。

S₁ 和 S₂ 是給定的模糊量詞。
S₃ 是需要確定的模糊量詞。

性情推理

在這種近似推理模式中，前件是可能包含模糊量詞“通常”的性情。量詞通常將性情推理和三段論推理聯絡起來；因此它起著重要的作用。

例如，性情推理中的投影推理規則可以表示如下：

通常( (L,M) 是 R ) ⇒ 通常 (L 是 [R ↓ L])

這裡[R ↓ L] 是模糊關係R在L上的投影

模糊邏輯規則庫

眾所周知，人類總是習慣於用自然語言進行交流。可以用以下自然語言表示式來表示人類知識：

如果前件那麼後件

如上所述的表示式稱為模糊 IF-THEN 規則庫。

規範形式

以下是模糊邏輯規則庫的規範形式：

規則 1 − 如果條件 C1，則限制 R1

規則 2 − 如果條件 C1，則限制 R2

規則 n − 如果條件 C1，則限制 Rn

模糊 IF-THEN 規則的解釋

模糊 IF-THEN 規則可以用以下四種形式解釋：

賦值語句

這類語句使用“=”（等於號）進行賦值。它們具有以下形式：

a = hello

climate = summer

條件語句

這類語句使用“IF-THEN”規則庫形式進行條件判斷。它們具有以下形式：

如果溫度很高，那麼氣候就炎熱

如果食物新鮮，那麼就吃。

無條件語句

它們具有以下形式：

GOTO 10

關閉風扇

語言變數

我們已經學習到模糊邏輯使用語言變數，語言變數是自然語言中的單詞或句子。例如，如果我們說溫度，它就是一個語言變數；它的值可以是很熱或很冷，稍微熱或稍微冷，很溫暖，稍微溫暖等等。單詞“很”、“稍微”是語言修飾詞。

語言變數的特徵

以下四個術語表徵語言變數：

變數名稱，通常用 x 表示。
變數的術語集，通常用 t(x) 表示。
生成變數 x 值的句法規則。
將 x 的每個值與其意義聯絡起來的語義規則。

模糊邏輯中的命題

我們知道命題是用任何語言表達的句子，通常以以下規範形式表達：

s 為 P

這裡，s 是主語，P 是謂語。

例如，“德里是印度的首府”，這是一個命題，其中“德里”是主語，“是印度的首府”是謂語，它顯示了主語的屬性。

我們知道邏輯是推理的基礎，模糊邏輯透過在模糊命題中使用模糊謂詞、模糊謂詞修飾詞、模糊量詞和模糊限定詞來擴充套件推理能力，這與經典邏輯不同。

模糊邏輯中的命題包括以下內容：

模糊謂詞

自然語言中幾乎每個謂詞都是模糊的，因此，模糊邏輯具有諸如高、矮、溫暖、熱、快等謂詞。

模糊謂詞修飾詞

我們在上面討論了語言修飾詞；我們還有許多模糊謂詞修飾詞充當修飾詞。它們對於生成語言變數的值至關重要。例如，單詞“很”、“稍微”是修飾詞，命題可以是“水稍微熱”。

模糊量詞

它可以定義為一個模糊數，它對一個或多個模糊或非模糊集合的基數進行模糊分類。它可以用來影響模糊邏輯中的機率。例如，單詞“許多”、“大多數”、“頻繁”用作模糊量詞，命題可以是“大多數人對此過敏”。

模糊限定詞

現在讓我們瞭解模糊限定詞。模糊限定詞也是模糊邏輯的命題。模糊限定具有以下形式：

基於真值的模糊限定

它宣告模糊命題的真值程度。

表示式 − 它表示為x 是 t。這裡，t 是模糊真值。

示例 − （汽車是黑色的）不是非常正確。

基於機率的模糊限定

它宣告模糊命題的機率，無論是數值還是區間。

表示式 − 它表示為x 是 λ。這裡，λ 是模糊機率。

示例 − （汽車是黑色的）可能是。

基於可能性的模糊限定

它宣告模糊命題的可能性。

表示式 − 它表示為x 是 π。這裡，π 是模糊可能性。

示例 − （汽車是黑色的）幾乎不可能。

模糊邏輯 - 推理系統

模糊推理系統是模糊邏輯系統的一個關鍵單元，其主要工作是決策。它使用“IF…THEN”規則以及連線詞“OR”或“AND”來制定必要的決策規則。

模糊推理系統的特性

以下是 FIS 的一些特性：

無論輸入是模糊的還是清晰的，FIS 的輸出始終是模糊集。
當用作控制器時，需要模糊輸出。
FIS 將配備一個去模糊單元，用於將模糊變數轉換為清晰變數。

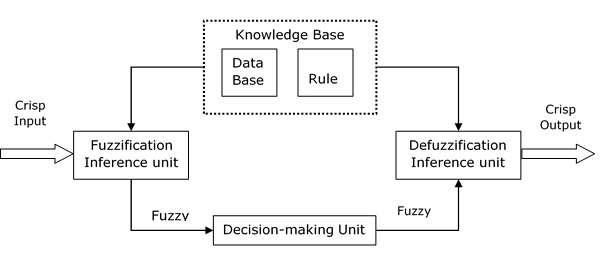
FIS 的功能模組

以下五個功能模組將幫助您瞭解 FIS 的構建：

規則庫 − 它包含模糊 IF-THEN 規則。
資料庫 − 它定義模糊規則中使用的模糊集的隸屬函式。
決策單元 − 它對規則進行運算。
模糊化介面單元 − 它將清晰量轉換為模糊量。
去模糊化介面單元 − 它將模糊量轉換為清晰量。以下是模糊干擾系統的框圖。

FIS 的工作原理

FIS 的工作原理包括以下步驟：

模糊化單元支援多種模糊化方法的應用，並將清晰輸入轉換為模糊輸入。
在將清晰輸入轉換為模糊輸入後，形成知識庫——規則庫和資料庫的集合。
去模糊單元將模糊輸入最終轉換為清晰輸出。

FIS 的方法

現在讓我們討論 FIS 的不同方法。以下是 FIS 的兩種重要方法，它們具有不同的模糊規則結果：

Mamdani 模糊推理系統
Takagi-Sugeno 模糊模型 (TS 方法)

Mamdani 模糊推理系統

該系統由Ebrahim Mamdani於1975年提出。其基本思想是透過綜合從系統操作人員那裡獲得的一組模糊規則來控制蒸汽機和鍋爐組合。

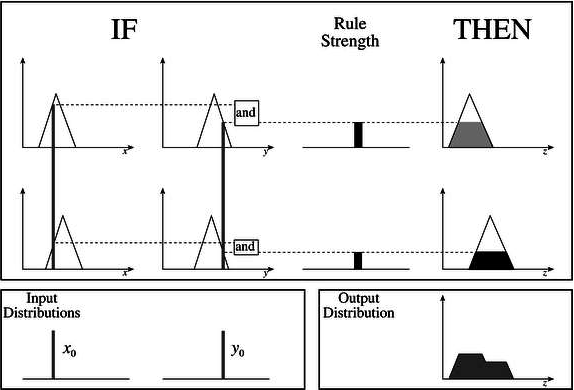
輸出計算步驟

要從該模糊推理系統（FIS）計算輸出，需要遵循以下步驟：

步驟1 − 此步驟需要確定模糊規則集。
步驟2 − 此步驟使用輸入隸屬函式將輸入模糊化。
步驟3 − 現在根據模糊規則，結合模糊化後的輸入來建立規則強度。
步驟4 − 此步驟透過結合規則強度和輸出隸屬函式來確定規則的結果。
步驟5 − 將所有結果結合起來以獲得輸出分佈。
步驟6 − 最後，獲得去模糊化的輸出分佈。

以下是Mamdani模糊介面系統的框圖。（此處應插入框圖）

Takagi-Sugeno 模糊模型 (TS 方法)

該模型由Takagi、Sugeno和Kang於1985年提出。規則格式如下：

如果x是A且y是B，則Z = f(x,y)

這裡，A和B是前件中的模糊集，z = f(x,y)是結果中的精確函式。

模糊推理過程

Takagi-Sugeno模糊模型（TS方法）下的模糊推理過程按以下方式進行：

步驟1：模糊化輸入 − 此處，將系統的輸入模糊化。
步驟2：應用模糊運算元 − 此步驟必須應用模糊運算元以獲得輸出。

Sugeno形式的規則格式

Sugeno形式的規則格式如下：

如果7 = x且9 = y，則輸出為z = ax+by+c

兩種方法的比較

現在讓我們瞭解Mamdani系統和Sugeno模型之間的比較。

輸出隸屬函式 − 兩者之間的主要區別在於輸出隸屬函式的基礎上。Sugeno輸出隸屬函式是線性的或常數的。
聚合和去模糊化過程 − 兩者之間的區別還在於模糊規則的結果，並且由於相同的原因，它們的聚合和去模糊化過程也不同。
數學規則 − Sugeno規則比Mamdani規則具有更多數學規則。
可調引數 − Sugeno控制器比Mamdani控制器具有更多可調引數。

模糊邏輯 - 資料庫和查詢

我們在之前的章節中學習過，模糊邏輯是一種基於“真值程度”而不是通常的“真或假”邏輯的計算方法。它處理的是近似的而不是精確的推理，以一種更類似於人類邏輯的方式解決問題，因此，布林代數的二值實現資料庫查詢過程是不夠的。

資料庫上關係的模糊場景

可以透過以下示例來理解資料庫上關係的模糊場景：

例子

假設我們有一個數據庫，其中包含訪問過印度的人員記錄。在簡單的資料庫中，我們將以以下方式進行條目：

姓名	年齡	國籍	訪問國家	停留天數	訪問年份
John Smith	35	美國	印度	41	1999
John Smith	35	美國	義大利	72	1999
John Smith	35	美國	日本	31	1999

現在，如果有人查詢99年訪問過印度和日本並且是美國公民的人，則輸出將顯示兩條包含John Smith姓名條目的記錄。這是一個簡單的查詢，生成簡單的輸出。

但是，如果我們想知道上述查詢中的人是否年輕呢？根據上述結果，該人的年齡為35歲。但是，我們可以假設此人年輕還是不年輕呢？同樣，相同的事情也可以應用於其他欄位，如停留天數、訪問年份等。

可以使用模糊值集來解決上述問題，如下所示：

FV(年齡){非常年輕，年輕，有點老，老}
FV(停留天數){幾乎幾天，幾天，相當幾天，許多天}
FV(訪問年份){遙遠的過去，最近的過去，最近}
現在，如果任何查詢具有模糊值，則結果也將具有模糊性。

模糊查詢系統

模糊查詢系統是一個使用者介面，用於使用（準）自然語言句子從資料庫獲取資訊。已經提出了許多模糊查詢實現，導致略微不同的語言。儘管根據不同實現的特殊性存在一些差異，但模糊查詢句子的答案通常是按匹配程度排序的記錄列表。

模糊邏輯 - 量化

在對自然語言語句建模時，量化語句起著重要作用。這意味著自然語言很大程度上依賴於量化結構，而量化結構通常包括模糊概念，如“幾乎所有”、“許多”等。以下是量化命題的一些示例：

每個學生都通過了考試。
每輛跑車都很貴。
許多學生通過了考試。
許多跑車都很貴。

在上述示例中，量詞“每個”和“許多”應用於清晰的限制“學生”以及清晰的範圍“(透過考試的)人”和“汽車”以及清晰的範圍“跑車”。

模糊事件、模糊均值和模糊方差

藉助一個例子，我們可以理解上述概念。讓我們假設我們是名為ABC公司的股東。目前，該公司每股股票售價為40盧比。還有三家業務與ABC類似的公司，但它們以不同的價格提供股票——每股100盧比、每股85盧比和每股60盧比。

現在，這種價格收購的機率分佈如下：

價格	100盧比	85盧比	60盧比
機率	0.3	0.5	0.2

(此處應插入機率值)

100 × 0.3 + 85 × 0.5 + 60 × 0.2 = 84.5

並且，根據標準機率論，上述分佈給出的預期價格方差如下：

(100 − 84.5)² × 0.3 + (85 − 84.5)² × 0.5 + (60 − 84.5)² × 0.2 = 124.825

假設100在這個集合中的隸屬度為0.7，85的隸屬度為1，60的隸屬度為0.5。這些可以反映在以下模糊集中：

$$ \left \{ \frac{0.7}{100}, \: \frac{1}{85}, \: \frac{0.5}{60} \right \} $$

以這種方式獲得的模糊集稱為模糊事件。

我們想要模糊事件的機率，我們的計算結果為：

0.7 × 0.3 + 1 × 0.5 + 0.5 × 0.2 = 0.21 + 0.5 + 0.1 = 0.81

現在，我們需要計算模糊均值和模糊方差，計算如下：

模糊均值 $= \left ( \frac{1}{0.81} \right ) × (100 × 0.7 × 0.3 + 85 × 1 × 0.5 + 60 × 0.5 × 0.2)$

$= 85.8$

模糊方差 $= 7496.91 − 7361.91 = 135.27$ (這個計算過程似乎有問題，需要核實)

模糊邏輯 - 決策

這是一種活動，其中包括為實現某個目標而需要採取的步驟，以從那些需要的替代方案中選擇合適的替代方案。

決策步驟

現在讓我們討論決策過程中涉及的步驟：

確定備選方案集 − 此步驟必須確定需要從中做出決策的備選方案。
評估備選方案 − 在這裡，必須評估備選方案，以便可以就其中一個備選方案做出決策。
比較備選方案 − 此步驟對評估的備選方案進行比較。

決策型別

現在我們將瞭解不同型別的決策。

個人決策

在這種型別的決策中，只有一人負責做出決策。在這種情況下，決策模型可以描述為：

可能的行動集
目標集 $G_i\left ( i \: \in \: X_n \right );$
約束集 $C_j\left ( j \: \in \: X_m \right )$

上述目標和約束用模糊集表示。

現在考慮集合A。那麼，該集合的目標和約束由下式給出：

$G_i\left ( a \right )$ = 複合 $\left [ G_i\left ( a \right ) \right ]$ = $G_i^1\left ( G_i\left ( a \right ) \right )$ with $G_i^1$

$C_j\left ( a \right )$ = 複合 $\left [ C_j\left ( a \right ) \right ]$ = $C_j^1\left ( C_j\left ( a \right ) \right )$ with $C_j^1$ 對於 $a\:\in \:A$

上述情況下的模糊決策由下式給出：

$$F_D = min[i\in X_{n}^{in}fG_i\left ( a \right ),j\in X_{m}^{in}fC_j\left ( a \right )]$$

多人決策

在這種情況下，決策包括幾個人，以便利用不同人的專業知識來做出決策。

計算如下：

偏好 $x_i$ 而不是 $x_j$ 的人數 = $N\left ( x_i, \: x_j \right )$

決策者總數 = $n$

然後，$SC\left ( x_i, \: x_j \right ) = \frac{N\left ( x_i, \: x_j \right )}{n}$

多目標決策

當存在多個要實現的目標時，就會發生多目標決策。這種型別的決策有兩個問題：

獲取與各種備選方案對目標滿意度的相關資訊。
權衡每個目標的相對重要性。

在數學上，我們可以定義一個n個備選方案的集合為：

$A = \left [ a_1, \:a_2,\:..., \: a_i, \: ..., \:a_n \right ]$

以及“m”個目標的集合為 $O = \left [ o_1, \:o_2,\:..., \: o_i, \: ..., \:o_n \right ]$

多屬性決策

當可以基於物件的多個屬性來進行備選方案的評估時，就會進行多屬性決策。屬性可以是數值資料、語言資料和定性資料。

在數學上，多屬性評估是基於以下線性方程進行的：

$$Y = A_1X_1+A_2X_2+...+A_iX_i+...+A_rX_r$$

模糊邏輯 - 控制系統

模糊邏輯在各種控制應用中都取得了巨大的成功。幾乎所有消費產品都具有模糊控制。一些例子包括使用空調控制室溫、車輛中使用的防抱死系統、交通燈控制、洗衣機、大型經濟系統等。

為什麼在控制系統中使用模糊邏輯

控制系統是由物理元件組成的裝置，旨在改變另一個物理系統，以便該系統表現出某些期望的特性。以下是在控制系統中使用模糊邏輯的一些原因：

在應用傳統控制時，需要了解以精確術語制定的模型和目標函式。這使得在許多情況下很難應用。
透過應用模糊邏輯控制，我們可以利用人類的專業知識和經驗來設計控制器。
模糊控制規則，基本上就是IF-THEN規則，可以最好地用於設計控制器。

模糊邏輯控制 (FLC) 設計中的假設

在設計模糊控制系統時，應做出以下六個基本假設：

系統是可觀測的和可控的 − 必須假設輸入、輸出以及狀態變數都可用於觀測和控制。
知識庫的存在 − 必須假設存在一個知識庫，其中包含語言規則和一組可以從中提取規則的輸入輸出資料集。
解的存在性 − 必須假設存在解。
“足夠好”的解就足夠了 − 控制工程應該尋找“足夠好”的解，而不是最優解。
精度範圍 − 模糊邏輯控制器必須設計在可接受的精度範圍內。
關於穩定性和最優性的問題 − 在設計模糊邏輯控制器時，穩定性和最優性的問題必須是開放的，而不是明確解決的。

模糊邏輯控制的架構

下圖顯示了模糊邏輯控制 (FLC) 的架構。

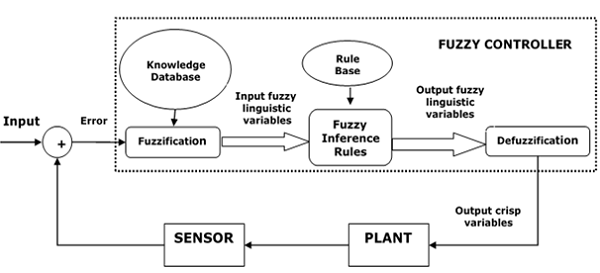
FLC 的主要組成部分

以下是上圖所示 FLC 的主要組成部分：

模糊化器 − 模糊化器的作用是將清晰的輸入值轉換為模糊值。
模糊知識庫 − 它儲存有關所有輸入輸出模糊關係的知識。它還具有隸屬函式，該函式將輸入變數定義為模糊規則庫，將輸出變數定義為被控物件。
模糊規則庫 − 它儲存有關過程或領域操作的知識。
推理引擎 − 它是任何 FLC 的核心。它基本上透過執行近似推理來模擬人類決策。
反模糊化器 − 反模糊化器的作用是從模糊推理引擎獲得模糊值並將其轉換為清晰值。

FLC 設計步驟

以下是 FLC 設計中涉及的步驟：

變數識別 − 在這裡，必須識別所考慮物件的輸入、輸出和狀態變數。
模糊子集配置 − 將資訊宇宙劃分為多個模糊子集，併為每個子集分配一個語言標籤。務必確保這些模糊子集包含宇宙的所有元素。
獲取隸屬函式 − 現在為我們在上述步驟中獲得的每個模糊子集獲得隸屬函式。
模糊規則庫配置 − 現在透過分配模糊輸入和輸出之間的關係來制定模糊規則庫。
模糊化 − 此步驟啟動模糊化過程。
組合模糊輸出 − 透過應用模糊近似推理，找到模糊輸出並將其合併。
反模糊化 − 最後，啟動反模糊化過程以形成清晰的輸出。

模糊邏輯控制的優點

現在讓我們討論模糊邏輯控制的優點。

更便宜 − 就效能而言，開發 FLC 比開發基於模型的控制器或其他控制器便宜。
魯棒性 − 由於 FLC 能夠覆蓋很大的執行條件範圍，因此它們比 PID 控制器更魯棒。
可定製性 − FLC 是可定製的。
模擬人類演繹思維 − FLC 的基本設計是模擬人類演繹思維，即人們用來從已知資訊中推斷結論的過程。
可靠性 − FLC 比傳統的控制系統更可靠。
效率 − 模糊邏輯應用於控制系統時效率更高。

模糊邏輯控制的缺點

我們現在將討論模糊邏輯控制的缺點。

需要大量資料 − FLC 需要大量資料才能應用。
適用於中等歷史資料的情況 − FLC 不適用於遠小於或遠大於歷史資料的程式。
需要很高的專業知識 − 這是一個缺點，因為系統的準確性取決於人類的知識和專業知識。
需要定期更新規則 − 規則必須隨著時間的推移而更新。

自適應模糊控制器

本章將討論什麼是自適應模糊控制器及其工作原理。自適應模糊控制器設計了一些可調引數以及用於調整它們的嵌入式機制。自適應控制器已被用於提高控制器的效能。

實施自適應演算法的基本步驟

現在讓我們討論實施自適應演算法的基本步驟。

收集可觀測資料 − 收集可觀測資料以計算控制器的效能。
調整控制器引數 − 現在，藉助控制器效能，將計算控制器引數的調整。
提高控制器效能 − 在此步驟中，調整控制器引數以提高控制器的效能。

操作概念

控制器的設計基於一個模擬真實系統的假設數學模型。計算實際系統與其數學表示之間的誤差，如果誤差相對較小，則認為該模型有效。

還存在一個閾值常數，它為控制器的有效性設定一個邊界。控制輸入被送入真實系統和數學模型。這裡，假設 $x\left ( t \right )$ 是真實系統的輸出，$y\left ( t \right )$ 是數學模型的輸出。然後可以計算誤差 $\epsilon \left ( t \right )$ 如下：

$$\epsilon \left ( t \right ) = x\left ( t \right ) - y\left ( t \right )$$

這裡，$x_{desired}$ 是我們想要從系統中獲得的輸出，$\mu \left ( t \right )$ 是來自控制器並進入真實系統和數學模型的輸出。

下圖顯示瞭如何跟蹤真實系統輸出和數學模型之間的誤差函式：

系統的引數化

基於模糊數學模型設計的模糊控制器將具有以下形式的模糊規則：

規則 1 − IF $x_1\left ( t_n \right )\in X_{11} \: AND...AND\: x_i\left ( t_n \right )\in X_{1i}$

THEN $\mu _1\left ( t_n \right ) = K_{11}x_1\left ( t_n \right ) + K_{12}x_2\left ( t_n \right ) \: +...+ \: K_{1i}x_i\left ( t_n \right )$

規則 2 − IF $x_1\left ( t_n \right )\in X_{21} \: AND...AND \: x_i\left ( t_n \right )\in X_{2i}$

THEN $\mu _2\left ( t_n \right ) = K_{21}x_1\left ( t_n \right ) + K_{22}x_2\left ( t_n \right ) \: +...+ \: K_{2i}x_i\left ( t_n \right ) $

規則 j − IF $x_1\left ( t_n \right )\in X_{k1} \: AND...AND \: x_i\left ( t_n \right )\in X_{ki}$

THEN $\mu _j\left ( t_n \right ) = K_{j1}x_1\left ( t_n \right ) + K_{j2}x_2\left ( t_n \right ) \: +...+ \: K_{ji}x_i\left ( t_n \right ) $

上述引數集表徵了控制器。

機制調整

調整控制器引數以提高控制器的效能。計算引數調整的過程是調整機制。

數學上，令 $\theta ^\left ( n \right )$ 為在時間 $t = t_n$ 時要調整的引數集。調整可以是引數的重新計算，

$$\theta ^\left ( n \right ) = \Theta \left ( D_0,\: D_1, \: ..., \:D_n \right )$$

這裡 $D_n$ 是在時間 $t = t_n$ 收集的資料。

現在，透過基於其先前值更新引數集來重新制定此公式，

$$\theta ^\left ( n \right ) = \phi ( \theta ^{n-1}, \: D_n)$$

選擇自適應模糊控制器的引數

選擇自適應模糊控制器需要考慮以下引數：

系統能否完全由模糊模型逼近？
如果系統可以完全由模糊模型逼近，則該模糊模型的引數是否容易獲得，或者必須線上確定？
如果系統不能完全由模糊模型逼近，它能否由一組模糊模型分段逼近？
如果系統可以由一組模糊模型逼近，這些模型是否具有相同的格式但引數不同，或者它們具有不同的格式？
如果系統可以由一組具有相同格式的模糊模型逼近，每個模型都有一組不同的引數，則這些引數集是否容易獲得，或者必須線上確定？

神經網路中的模糊性

人工神經網路 (ANN) 是一個高效的計算系統網路，其核心主題借鑑了生物神經網路的類比。人工神經網路也稱為“人工神經系統”、“並行分散式處理系統”、“連線主義系統”。人工神經網路獲取大量單元，這些單元以某種模式互連，以允許單元之間進行通訊。這些單元也稱為節點或神經元，是並行工作的簡單處理器。

每個神經元都透過連線鏈與其他神經元連線。每個連線鏈都與一個權重相關聯，該權重包含有關輸入訊號的資訊。這是神經元解決特定問題最有用的資訊，因為權重通常會抑制正在傳輸的訊號。每個神經元都有其內部狀態，稱為啟用訊號。在組合輸入訊號和啟用規則後產生的輸出訊號可能會發送到其他單元。它還包括一個偏差“b”，其權重始終為 1。

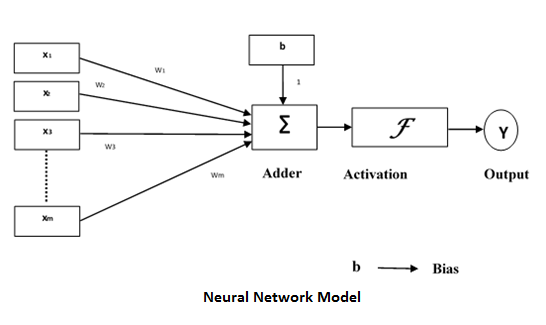
為什麼在神經網路中使用模糊邏輯

正如我們上面所討論的，人工神經網路中的每個神經元都透過連線鏈與其他神經元連線，並且該鏈與一個包含有關輸入訊號資訊的權重相關聯。因此，我們可以說權重包含有關輸入的有用資訊以解決問題。

以下是神經網路中使用模糊邏輯的一些原因：

模糊邏輯主要用於在神經網路中從模糊集定義權重。
當無法應用清晰值時，使用模糊值。
我們已經學習過，訓練和學習有助於神經網路在意外情況下表現更好。那時，模糊值比清晰值更適用。
當我們在神經網路中使用模糊邏輯時，值一定不能是清晰的，並且可以並行進行處理。

模糊認知圖

它是一種神經網路中的模糊性形式。基本上，FCM就像一個具有模糊狀態（不僅僅是1或0）的動態狀態機。

在神經網路中使用模糊邏輯的困難

儘管具有眾多優點，但在神經網路中使用模糊邏輯時也存在一些困難。困難與隸屬度規則有關，需要構建模糊系統，因為有時很難根據給定的複雜資料集推匯出它。

神經網路訓練的模糊邏輯

神經網路和模糊邏輯之間的反向關係，即使用神經網路訓練模糊邏輯也是一個很好的研究領域。以下是構建神經網路訓練的模糊邏輯的兩個主要原因：

藉助神經網路可以輕鬆學習新的資料模式，因此可以用於預處理模糊系統中的資料。
神經網路由於其能夠學習新的輸入資料的新關係的能力，可以用來改進模糊規則以建立模糊自適應系統。

神經網路訓練的模糊系統的示例

神經網路訓練的模糊系統正在許多商業應用中使用。讓我們看看一些應用神經網路訓練的模糊系統的例子：

位於日本橫濱的國際模糊工程研究實驗室 (LIFE) 擁有一個反向傳播神經網路，可以推匯出模糊規則。該系統已成功應用於外匯交易系統，大約有 5000 條模糊規則。
福特汽車公司已經開發出用於汽車怠速控制的可訓練模糊系統。
國家半導體公司的軟體產品 NeuFuz 支援使用神經網路為控制應用生成模糊規則。
德國的 AEG 公司在其節水節能機器中使用神經網路訓練的模糊控制系統。它共有 157 條模糊規則。

模糊邏輯 - 應用

在本章中，我們將討論模糊邏輯概念被廣泛應用的領域。

航空航天

在航空航天領域，模糊邏輯用於以下領域：

航天器的姿態控制
衛星高度控制
飛機除冰車輛中的流量和混合物調節

汽車

在汽車領域，模糊邏輯用於以下領域：

用於怠速控制的可訓練模糊系統
自動變速器的換檔排程方法
智慧高速公路系統
交通控制
提高自動變速器的效率

商業

在商業領域，模糊邏輯用於以下領域：

決策支援系統
大公司的人員評估

國防

在國防領域，模糊邏輯用於以下領域：

水下目標識別
熱紅外影像的自動目標識別
海軍決策支援工具
超高速攔截器的控制
北約決策的模糊集建模

電子

在電子領域，模糊邏輯用於以下領域：

控制攝像機的自動曝光
潔淨室的溼度控制
空調系統
洗衣機定時
微波爐
真空吸塵器

金融

在金融領域，模糊邏輯用於以下領域：

鈔票轉賬控制
資金管理
股市預測

工業部門

在工業領域，模糊邏輯用於以下領域：

水泥窯控制、熱交換器控制
活性汙泥汙水處理過程控制
水淨化廠控制
工業質量保證的定量模式分析
結構設計中約束滿足問題的控制
水淨化廠控制

製造業

在製造業中，模糊邏輯用於以下領域：

乳酪生產最佳化
牛奶生產最佳化

海洋

在海洋領域，模糊邏輯用於以下領域：

船舶自動駕駛儀
最佳航線選擇
自主水下航行器的控制
船舶操縱

醫療

在醫療領域，模糊邏輯用於以下領域：

醫療診斷支援系統
麻醉期間動脈壓力的控制
麻醉的多變數控制
阿爾茨海默病患者神經病理學發現的建模
放射學診斷
糖尿病和前列腺癌的模糊推理診斷

證券

在證券領域，模糊邏輯用於以下領域：

證券交易決策系統
各種安全裝置

交通運輸

在交通運輸領域，模糊邏輯用於以下領域：

自動地下列車執行
列車時刻表控制
鐵路加速
制動和停車

模式識別與分類

在模式識別與分類中，模糊邏輯用於以下領域：

基於模糊邏輯的語音識別
基於模糊邏輯的
手寫識別
基於模糊邏輯的面部特徵分析
命令分析
模糊影像搜尋

心理學

在心理學領域，模糊邏輯用於以下領域：

基於模糊邏輯的人類行為分析
基於模糊邏輯推理的犯罪調查和預防

列印頁面