
- 離散數學資源
- 離散數學 - 快速指南
- 離散數學 - 資源
- 離散數學 - 討論
離散數學 - 圖論進階
圖著色
圖著色是指為圖 G 的每個頂點分配顏色的過程,使得沒有相鄰的頂點具有相同的顏色。目標是在著色圖時最小化顏色的數量。為著色圖 G 所需的最少顏色數稱為該圖的色數。圖著色問題是一個 NP 完全問題。
圖著色方法
為具有 n 個頂點的圖 G 著色的步驟如下:
步驟 1 - 按某種順序排列圖的頂點。
步驟 2 - 選擇第一個頂點並用第一種顏色對其進行著色。
步驟 3 - 選擇下一個頂點,並用與其相鄰的任何頂點都沒有著色的最低編號的顏色對其進行著色。如果所有相鄰頂點都用此顏色著色,則為其分配一個新顏色。重複此步驟,直到所有頂點都著色。
示例
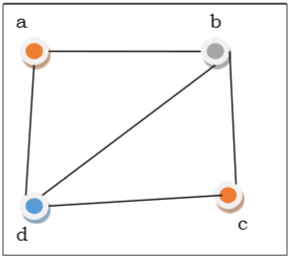
在上圖中,首先將頂點 $a$ 著色為紅色。由於頂點 a 的相鄰頂點再次相鄰,因此頂點 $b$ 和頂點 $d$ 用不同的顏色著色,分別為綠色和藍色。然後將頂點 $c$ 著色為紅色,因為 $c$ 的任何相鄰頂點都沒有著色為紅色。因此,我們可以用 3 種顏色對圖進行著色。因此,該圖的色數為 3。
圖著色的應用
圖著色的一些應用包括:
圖遍歷
圖遍歷是按照某種系統順序訪問圖的所有頂點的問題。主要有兩種遍歷圖的方法。
- 廣度優先搜尋
- 深度優先搜尋
廣度優先搜尋
廣度優先搜尋 (BFS) 從圖 $G$ 的起始層級 0 頂點 $X$ 開始。然後我們訪問 $X$ 的所有鄰居頂點。訪問後,我們將頂點標記為“已訪問”,並將它們放入層級 1。然後我們從層級 1 頂點開始,對每個層級 1 頂點應用相同的方法,依此類推。當圖的每個頂點都被訪問後,BFS 遍歷終止。
BFS 演算法
其概念是在訪問鄰居頂點的其他鄰居頂點之前訪問所有鄰居頂點。
將所有節點的狀態初始化為“就緒”。
將源頂點放入佇列中,並將狀態更改為“等待”。
重複以下兩個步驟,直到佇列為空:
從佇列中刪除第一個頂點,並將其標記為“已訪問”。
將狀態為“就緒”的已刪除頂點的所有鄰居新增到佇列的尾部。將其狀態標記為“等待”。
問題
讓我們取一個圖(源頂點為“a”),並應用 BFS 演算法找出遍歷順序。

解決方案 -
將所有頂點狀態初始化為“就緒”。
將 a 放入佇列中,並將狀態更改為“等待”。
從佇列中刪除 a,將其標記為“已訪問”。
將 a 的狀態為“就緒”的鄰居 b、d 和 e 新增到佇列的末尾,並將它們標記為“等待”。
從佇列中刪除 b,將其標記為“已訪問”,將狀態為“就緒”的鄰居 c 放入佇列的末尾,並將 c 標記為“等待”。
從佇列中刪除 d,並將其標記為“已訪問”。它沒有狀態為“就緒”的鄰居。
從佇列中刪除 e,並將其標記為“已訪問”。它沒有狀態為“就緒”的鄰居。
從佇列中刪除 c,並將其標記為“已訪問”。它沒有狀態為“就緒”的鄰居。
佇列為空,因此停止。
因此,遍歷順序為:
$a \rightarrow b \rightarrow d \rightarrow e \rightarrow c$
遍歷的替代順序為:
$a \rightarrow b \rightarrow e \rightarrow d \rightarrow c$
或者,$a \rightarrow d \rightarrow b \rightarrow e \rightarrow c$
或者,$a \rightarrow e \rightarrow b \rightarrow d \rightarrow c$
或者,$a \rightarrow b \rightarrow e \rightarrow d \rightarrow c$
或者,$a \rightarrow d \rightarrow e \rightarrow b \rightarrow c$
BFS 的應用
- 查詢最短路徑
- 無權圖的最小生成樹
- GPS 導航系統
- 檢測無向圖中的迴圈
- 查詢一個連通分量內的所有節點
複雜度分析
令 $G(V, E)$ 為一個具有 $|V|$ 個頂點和 $|E|$ 條邊的圖。如果廣度優先搜尋演算法訪問圖中的每個頂點並檢查每條邊,則其時間複雜度為:
$$O( | V | + | E | ). O( | E | )$$
它可能在 $O(1)$ 和 $O(|V2|)$ 之間變化
深度優先搜尋
深度優先搜尋 (DFS) 演算法從頂點 $v$ 開始,然後遍歷到其之前未訪問過的相鄰頂點(例如 x),並將其標記為“已訪問”,然後繼續遍歷 x 的相鄰頂點,依此類推。
如果在任何頂點處遇到所有相鄰頂點都已訪問,則它會回溯,直到找到第一個具有未遍歷過的相鄰頂點的頂點。然後,它遍歷該頂點,繼續遍歷其相鄰頂點,直到遍歷所有已訪問的頂點並且必須再次回溯。透過這種方式,它將遍歷從初始頂點 $v$ 可到達的所有頂點。
DFS 演算法
其概念是在訪問鄰居頂點的其他鄰居頂點之前訪問所有鄰居頂點。
將所有節點的狀態初始化為“就緒”
將源頂點放入堆疊中,並將狀態更改為“等待”
重複以下兩個步驟,直到堆疊為空:
從堆疊中彈出頂部的頂點,並將其標記為“已訪問”
將狀態為“就緒”的已刪除頂點的所有鄰居推送到堆疊的頂部。將其狀態標記為“等待”。
問題
讓我們取一個圖(源頂點為“a”),並應用 DFS 演算法找出遍歷順序。

解決方案
將所有頂點狀態初始化為“就緒”。
將 a 推入堆疊中,並將狀態更改為“等待”。
彈出 a 並將其標記為“已訪問”。
將 a 的狀態為“就緒”的鄰居 e、d 和 b 推送到堆疊的頂部,並將它們標記為“等待”。
從堆疊中彈出 b,將其標記為“已訪問”,將狀態為“就緒”的鄰居 c 推送到堆疊中。
從堆疊中彈出 c 並將其標記為“已訪問”。它沒有“就緒”的鄰居。
從堆疊中彈出 d 並將其標記為“已訪問”。它沒有“就緒”的鄰居。
從堆疊中彈出 e 並將其標記為“已訪問”。它沒有“就緒”的鄰居。
堆疊為空。因此停止。
因此,遍歷順序為:
$a \rightarrow b \rightarrow c \rightarrow d \rightarrow e$
遍歷的替代順序為:
$a \rightarrow e \rightarrow b \rightarrow c \rightarrow d$
或者,$a \rightarrow b \rightarrow e \rightarrow c \rightarrow d$
或者,$a \rightarrow d \rightarrow e \rightarrow b \rightarrow c$
或者,$a \rightarrow d \rightarrow c \rightarrow e \rightarrow b$
或者,$a \rightarrow d \rightarrow c \rightarrow b \rightarrow e$
複雜度分析
令 $G(V, E)$ 為一個具有 $|V|$ 個頂點和 $|E|$ 條邊的圖。如果 DFS 演算法訪問圖中的每個頂點並檢查每條邊,則時間複雜度為:
$$\circleddash ( | V | + | E | )$$
應用
- 檢測圖中的迴圈
- 查詢拓撲排序
- 測試圖是否為二分圖
- 查詢連通分量
- 查詢圖的橋
- 查詢圖中的雙連通性
- 解決騎士巡遊問題
- 解決只有一個解決方案的謎題