
離散數學速查指南
離散數學 - 導論
數學可以大致分為兩類:
連續數學 - 它基於連續數軸或實數。其特點是任意兩數之間幾乎總存在無限多個數。例如,連續數學中的函式可以用一條沒有間斷的光滑曲線繪製。
離散數學 - 它涉及離散值;即任意兩點之間只有可數個點。例如,如果我們有一組有限的物件,則該函式可以定義為這些物件的序偶列表,並且可以表示為這些序偶的完整列表。
離散數學中的主題
雖然離散數學的分支數量無法確定,但在任何關於此問題的研究中,幾乎總是會涵蓋以下主題:
- 集合、關係和函式
- 數理邏輯
- 群論
- 計數理論
- 機率
- 數學歸納法和遞推關係
- 圖論
- 樹
- 布林代數
我們將在本教程的後續章節中討論這些概念。
離散數學 - 集合
德國數學家G. 康托爾引入了集合的概念。他將集合定義為透過某種規則或描述選擇的確定且可區分物件的集合。
集合理論構成了計數理論、關係、圖論和有限狀態機等其他幾個研究領域的基礎。在本章中,我們將介紹集合論的不同方面。
集合 - 定義
集合是不同元素的無序集合。集合可以用集合括號列出其元素來明確地寫出。如果元素的順序改變或集合的任何元素重複,則不會對集合產生任何改變。
集合的一些例子
- 所有正整數的集合
- 太陽系中所有行星的集合
- 印度所有邦的集合
- 所有小寫字母的集合
集合的表示
集合可以用兩種方式表示:
- 列舉法或表格法
- 集合構造器表示法
列舉法或表格法
集合透過列出構成它的所有元素來表示。元素用大括號括起來,並用逗號分隔。
例1 - 英文字母表中母音的集合,$A = \lbrace a,e,i,o,u \rbrace$
例2 - 小於10的奇數集合,$B = \lbrace 1,3,5,7,9 \rbrace$
集合構造器表示法
集合透過指定集合元素共有的屬性來定義。集合描述為 $A = \lbrace x : p(x) \rbrace$
例1 - 集合 $\lbrace a,e,i,o,u \rbrace$ 寫作:
$A = \lbrace x : \text{x是英文字母表中的母音} \rbrace$
例2 - 集合 $\lbrace 1,3,5,7,9 \rbrace$ 寫作:
$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$
如果元素x是集合S的成員,則表示為$x \in S$;如果元素y不是集合S的成員,則表示為$y \notin S$。
例 - 如果 $S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ 但 $1.5 \notin S$
一些重要的集合
N - 所有自然數的集合 = $\lbrace1, 2, 3, 4, .....\rbrace$
Z - 所有整數的集合 = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$
Z+ - 所有正整數的集合
Q - 所有有理數的集合
R - 所有實數的集合
W - 所有全數的集合
集合的基數
集合S的基數,用$|S|$表示,是集合的元素個數。這個數也稱為基數。如果一個集合有無限多個元素,則其基數為$\infty$。
例 - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$
如果有兩個集合X和Y,
$|X| = |Y|$ 表示兩個集合X和Y具有相同的基數。當X中的元素個數正好等於Y中的元素個數時,就會發生這種情況。在這種情況下,存在從X到Y的雙射函式'f'。
$|X| \le |Y|$ 表示集合X的基數小於或等於集合Y的基數。當X中的元素個數小於或等於Y中的元素個數時,就會發生這種情況。在這裡,存在從X到Y的單射函式'f'。
$|X| \lt |Y|$ 表示集合X的基數小於集合Y的基數。當X中的元素個數小於Y中的元素個數時,就會發生這種情況。在這裡,從X到Y的函式'f'是單射函式,但不是雙射函式。
$如果\ |X| \le |Y| 和 |X| \ge |Y| 則 |X| = |Y|。集合X和Y通常被稱為等價集合。
集合的型別
集合可以分為多種型別。其中一些是有限集、無限集、子集、全集、真子集、單元素集等。
有限集
包含確定數量元素的集合稱為有限集。
例 - $S = \lbrace x \:| \:x \in N$ and $70 \gt x \gt 50 \rbrace$
無限集
包含無限多個元素的集合稱為無限集。
例 - $S = \lbrace x \: | \: x \in N $ and $ x \gt 10 \rbrace$
子集
如果集合X的每個元素都是集合Y的元素,則集合X是集合Y的子集(寫成$X \subseteq Y$)。
例1 - 令,$X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 和 $Y = \lbrace 1, 2 \rbrace$。這裡集合Y是集合X的子集,因為集合Y的所有元素都在集合X中。因此,我們可以寫成$Y \subseteq X$。
例2 - 令,$X = \lbrace 1, 2, 3 \rbrace$ 和 $Y = \lbrace 1, 2, 3 \rbrace$。這裡集合Y是集合X的子集(不是真子集),因為集合Y的所有元素都在集合X中。因此,我們可以寫成$Y \subseteq X$。
真子集
“真子集”可以定義為“子集但不等”。如果集合X的每個元素都是集合Y的元素並且$|X| \lt |Y|$,則集合X是集合Y的真子集(寫成$ X \subset Y $)。
例 - 令,$X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 和 $Y = \lbrace 1, 2 \rbrace$。這裡集合$Y \subset X$,因為Y中的所有元素也包含在X中,並且X至少比集合Y多一個元素。
全集
它是特定上下文或應用程式中所有元素的集合。該上下文或應用程式中的所有集合本質上都是這個全集的子集。全集表示為$U$。
例 - 我們可以將$U$定義為地球上所有動物的集合。在這種情況下,所有哺乳動物的集合是$U$的子集,所有魚類的集合是$U$的子集,所有昆蟲的集合是$U$的子集,等等。
空集或零集
空集不包含任何元素。它用$\emptyset$表示。由於空集中的元素數量是有限的,因此空集是有限集。空集或零集的基數為零。
例 - $S = \lbrace x \:| \: x \in N$ and $7 \lt x \lt 8 \rbrace = \emptyset$
單元素集或單元集
單元素集或單元集只包含一個元素。單元素集用$\lbrace s \rbrace$表示。
例 - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$
相等集
如果兩個集合包含相同的元素,則稱它們相等。
例 - 如果$A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 6, 1, 2 \rbrace$,則它們相等,因為集合A的每個元素都是集合B的元素,集合B的每個元素都是集合A的元素。
等價集
如果兩個集合的基數相同,則稱它們為等價集。
例 - 如果$A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 16, 17, 22 \rbrace$,則它們是等價的,因為A的基數等於B的基數。即$|A| = |B| = 3$
重疊集
至少有一個公共元素的兩個集合稱為重疊集。
對於重疊集:
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
$n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$
$n(A) = n(A - B) + n(A \cap B)$
$n(B) = n(B - A) + n(A \cap B)$
例 - 令,$A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 6, 12, 42 \rbrace$。有一個公共元素'6',因此這些集合是重疊集。
不相交集
如果兩個集合A和B沒有任何公共元素,則稱它們為不相交集。因此,不相交集具有以下性質:
$n(A \cap B) = \emptyset$
$n(A \cup B) = n(A) + n(B)$
例 - 令,$A = \lbrace 1, 2, 6 \rbrace$ 和 $B = \lbrace 7, 9, 14 \rbrace$,沒有一個公共元素,因此這些集合是不相交集。
維恩圖
維恩圖是由John Venn於1880年發明的,它是一個示意圖,顯示了不同數學集合之間所有可能的邏輯關係。
例子
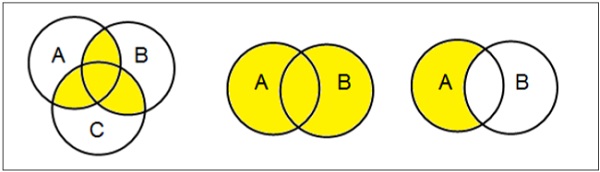
集合運算
集合運算包括集合並、集合交、集合差、集合補和笛卡爾積。
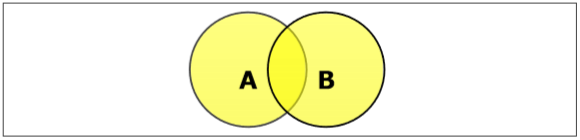
集合並
集合A和B的並集(用$A \cup B$表示)是屬於A、屬於B或同時屬於A和B的元素的集合。因此,$A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$。
例 - 如果$A = \lbrace 10, 11, 12, 13 \rbrace$ 和 B = $\lbrace 13, 14, 15 \rbrace$,則$A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$。(公共元素只出現一次)
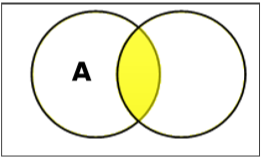
集合交集
集合 A 和 B 的交集(記作 $A \cap B$)是既屬於 A 又屬於 B 的元素的集合。因此,$A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$。
示例 − 如果 $A = \lbrace 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$,則 $A \cap B = \lbrace 13 \rbrace$。
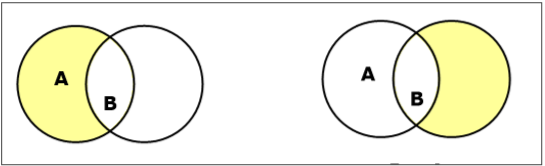
集合差/相對補集
集合 A 和 B 的集合差(記作 $A – B$)是隻屬於 A 但不屬於 B 的元素的集合。因此,$A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$。
示例 − 如果 $A = \lbrace 10, 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$,則 $(A - B) = \lbrace 10, 11, 12 \rbrace$ 且 $(B - A) = \lbrace 14, 15 \rbrace$。這裡我們可以看到 $(A - B) \ne (B - A)$
集合的補集
集合 A 的補集(記作 $A’$)是不屬於集合 A 的元素的集合。因此,$A' = \lbrace x | x \notin A \rbrace$。
更具體地說,$A'= (U - A)$,其中 $U$ 是包含所有物件的全集。
示例 − 如果 $A = \lbrace x \:| \: x\ \: {屬於奇數整數集合} \rbrace$,則 $A' = \lbrace y\: | \: y\ \: {不屬於奇數整數集合} \rbrace$
笛卡爾積/叉積
n 個集合 $A_1, A_2, \dots A_n$ 的笛卡爾積記作 $A_1 \times A_2 \dots \times A_n$,可以定義為所有可能的序對 $(x_1, x_2, \dots x_n)$,其中 $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$
示例 − 如果我們取兩個集合 $A = \lbrace a, b \rbrace$ 和 $B = \lbrace 1, 2 \rbrace$,
A 和 B 的笛卡爾積寫成 − $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$
B 和 A 的笛卡爾積寫成 − $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$
冪集
集合 S 的冪集是 S 的所有子集的集合,包括空集。基數為 n 的集合 S 的冪集的基數為 $2^n$。冪集記作 $P(S)$。
示例 −
對於集合 $S = \lbrace a, b, c, d \rbrace$,讓我們計算子集 −
包含 0 個元素的子集 − $\lbrace \emptyset \rbrace$(空集)
包含 1 個元素的子集 − $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$
包含 2 個元素的子集 − $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$
包含 3 個元素的子集 − $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$
包含 4 個元素的子集 − $\lbrace a, b, c, d \rbrace$
因此,$P(S)=$
$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$
$| P(S) | = 2^4 = 16$
注意 − 空集的冪集也是空集。
$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$
集合的劃分
集合 S 的劃分是 n 個不相交子集(例如 $P_1, P_2, \dots P_n$)的集合,滿足以下三個條件:
$P_i$ 不包含空集。
$\lbrack P_i \ne \lbrace \emptyset \rbrace\ 對所有\ 0 \lt i \le n \rbrack$
子集的並集必須等於整個原始集合。
$\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$
任意兩個不同的集合的交集為空集。
$\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ 對 a \ne b\ 其中 n \ge a,\: b \ge 0 \rbrack$
示例
設 $S = \lbrace a, b, c, d, e, f, g, h \rbrace$
一個可能的劃分是 $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$
另一個可能的劃分是 $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$
貝爾數
貝爾數給出劃分集合的方法數量。它們記作 $B_n$,其中 n 是集合的基數。
示例 −
設 $S = \lbrace 1, 2, 3\rbrace$,$n = |S| = 3$
另一種劃分是 −
1. $\emptyset , \lbrace 1, 2, 3 \rbrace$
2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$
3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$
4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$
5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$
因此 $B_3 = 5$
離散數學 - 關係
每當討論集合時,集合元素之間的關係就是接下來要討論的事情。集合內物件之間或兩個或多個集合的物件之間可能存在關係。
定義和性質
從集合 x 到 y 的二元關係 R(寫成 $xRy$ 或 $R(x,y)$)是笛卡爾積 $x \times y$ 的一個子集。如果 G 的有序對反轉,關係也會改變。
一般來說,集合 $A_1, \dots ,\ 和\ A_n$ 之間的 n 元關係 R 是 n 元積 $A_1 \times \dots \times A_n$ 的一個子集。在這種情況下,關係 R 的最小基數為零,最大基數為 $n^2$。
單個集合 A 上的二元關係 R 是 $A \times A$ 的一個子集。
對於兩個不同的集合 A 和 B,其基數分別為 *m* 和 *n*,從 A 到 B 的關係 R 的最大基數為 *mn*。
定義域和值域
如果有兩個集合 A 和 B,並且關係 R 有序對 (x, y),則:
R 的定義域 Dom(R) 是集合 $\lbrace x \:| \: (x, y) \in R \:對於某個 y\ 在\ B 中 \rbrace$
R 的值域 Ran(R) 是集合 $\lbrace y\: |\: (x, y) \in R \:對於某個 x\ 在\ A 中 \rbrace$
例子
設,$A = \lbrace 1, 2, 9 \rbrace $ 且 $ B = \lbrace 1, 3, 7 \rbrace$
情況 1 − 如果關係 R 是“等於”,則 $R = \lbrace (1, 1), (3, 3) \rbrace$
Dom(R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
情況 2 − 如果關係 R 是“小於”,則 $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
Dom(R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
情況 3 − 如果關係 R 是“大於”,則 $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
Dom(R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
使用圖形表示關係
關係可以使用有向圖來表示。
圖中頂點的數量等於定義關係的集合中元素的數量。對於關係 R 中的每個有序對 (x, y),都會有一條從頂點“x”到頂點“y”的有向邊。如果存在有序對 (x, x),則頂點“x”上將會有自環。
假設,集合 $S = \lbrace 1, 2, 3 \rbrace$ 上存在關係 $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$,它可以用下圖表示:
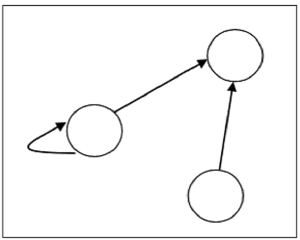
關係的型別
集合 X 和 Y 之間或 E 上的空關係是空集 $\emptyset$
集合 X 和 Y 之間的全關係是集合 $X \times Y$
集合 X 上的恆等關係是集合 $\lbrace (x, x) | x \in X \rbrace$
關係 R 的逆關係 R' 定義為 − $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
示例 − 如果 $R = \lbrace (1, 2), (2, 3) \rbrace$,則 $R'$ 將為 $\lbrace (2, 1), (3, 2) \rbrace$
如果 $\forall a \in A$ 與 a 相關(成立 aRa),則集合 A 上的關係 R 稱為自反的
示例 − 集合 $X = \lbrace a, b \rbrace$ 上的關係 $R = \lbrace (a, a), (b, b) \rbrace$ 是自反的。
如果不存在 $a \in A$ 與 a 相關(不成立 aRa),則集合 A 上的關係 R 稱為反自反的。
示例 − 集合 $X = \lbrace a, b \rbrace$ 上的關係 $R = \lbrace (a, b), (b, a) \rbrace$ 是反自反的。
如果 $xRy$ 蘊含 $yRx$,$\forall x \in A$ 且 $\forall y \in A$,則集合 A 上的關係 R 稱為對稱的。
示例 − 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的關係 $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ 是對稱的。
如果 $xRy$ 且 $yRx$ 蘊含 $x = y \: \forall x \in A$ 且 $\forall y \in A$,則集合 A 上的關係 R 稱為反對稱的。
示例 − 關係 $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ 是反對稱的,因為 $x \leq y$ 且 $y \leq x$ 蘊含 $x = y$。
如果 $xRy$ 且 $yRz$ 蘊含 $xRz, \forall x,y,z \in A$,則集合 A 上的關係 R 稱為傳遞的。
示例 − 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的關係 $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ 是傳遞的。
如果關係是自反的、對稱的和傳遞的,則它是等價關係。
示例 − 集合 $A = \lbrace 1, 2, 3 \rbrace$ 上的關係 $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ 是等價關係,因為它既是自反的、對稱的,又是傳遞的。
離散數學 - 函式
函式將集合的每個元素精確地分配給相關集合的一個元素。函式在各個領域都有其應用,例如表示演算法的計算複雜度、計數物件、研究序列和字串等。本部分的第三章也是最後一章重點介紹了函式的重要方面。
函式 - 定義
函式或對映(定義為 $f: X \rightarrow Y$)是從一個集合 X 的元素到另一個集合 Y 的元素的關係(X 和 Y 是非空集合)。X 稱為函式 'f' 的定義域,Y 稱為函式 'f' 的陪域。
函式 'f' 是 X 和 Y 上的關係,使得對於每個 $x \in X$,都存在唯一的 $y \in Y$,使得 $(x,y) \in R$。“x”稱為原像,“y”稱為函式 f 的像。
函式可以是一對一的或多對一的,但不能是一對多的。
單射/一對一函式
如果對於每個 $b \in B$,最多存在一個 $a \in A$ 使得 $f(s) = t$,則函式 $f: A \rightarrow B$ 是單射或一對一函式。
這意味著如果 $a_1 \ne a_2$ 蘊含 $f(a1) \ne f(a2)$,則函式f是單射的。
示例
$f: N \rightarrow N, f(x) = 5x$ 是單射的。
$f: N \rightarrow N, f(x) = x^2$ 是單射的。
$f: R\rightarrow R, f(x) = x^2$ 不是單射的,因為 $(-x)^2 = x^2$
滿射/到函式
函式 $f: A \rightarrow B$ 是滿射(映上)的,如果 f 的像等於其值域。等價地,對於每一個 $b \in B$,都存在某個 $a \in A$ 使得 $f(a) = b$。這意味著對於 B 中的任何 y,都存在 A 中的某個 x 使得 $y = f(x)$。
示例
$f : N \rightarrow N, f(x) = x + 2$ 是滿射的。
$f : R \rightarrow R, f(x) = x^2$ 不是滿射的,因為我們找不到一個平方為負數的實數。
雙射/一一對應
函式 $f: A \rightarrow B$ 是雙射或一一對應的,當且僅當 **f** 既是單射又是滿射。
問題
證明由 $f(x) = 2x – 3$ 定義的函式 $f: R \rightarrow R$ 是雙射函式。
**解釋** − 我們必須證明此函式既是單射又是滿射。
如果 $f(x_1) = f(x_2)$,則 $2x_1 – 3 = 2x_2 – 3$,這意味著 $x_1 = x_2$。
因此,f 是 **單射** 的。
這裡,$2x – 3= y$
所以,$x = (y+3)/2$,屬於 R,並且 $f(x) = y$。
因此,f 是 **滿射** 的。
由於 **f** 既是 **滿射** 又 是 **單射** 的,所以我們可以說 **f** 是 **雙射** 的。
函式的反函式
一一對應函式 $f : A \rightarrow B$ 的 **反函式** 是函式 $g : B \rightarrow A$,它滿足以下性質 −
$f(x) = y \Leftrightarrow g(y) = x$
如果存在反函式 g,則稱函式 f 可逆。
示例
函式 $f : Z \rightarrow Z, f(x)=x+5$ 是可逆的,因為它具有反函式 $ g : Z \rightarrow Z, g(x)= x-5$。
函式 $f : Z \rightarrow Z, f(x)=x^2$ 不可逆,因為它不是一一對應的,因為 $(-x)^2=x^2$。
函式的複合
兩個函式 $f: A \rightarrow B$ 和 $g: B \rightarrow C$ 可以複合得到一個複合函式 $g o f$。這是一個從 A 到 C 的函式,定義為 $(gof)(x) = g(f(x))$
示例
設 $f(x) = x + 2$ 和 $g(x) = 2x + 1$,求 $( f o g)(x)$ 和 $( g o f)(x)$。
解答
$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$
$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$
因此,$(f o g)(x) \neq (g o f)(x)$
關於複合的一些事實
如果 f 和 g 是一一對應的,則函式 $(g o f)$ 也是一一對應的。
如果 f 和 g 是滿射的,則函式 $(g o f)$ 也是滿射的。
複合總是滿足結合律,但不滿足交換律。
離散數學 - 命題邏輯
數學邏輯的規則指定了推理數學命題的方法。希臘哲學家亞里士多德是邏輯推理的先驅。邏輯推理為許多數學領域以及計算機科學提供了理論基礎。它在計算機科學中有很多實際應用,例如計算機器的設計、人工智慧、程式語言的資料結構的定義等。
**命題邏輯**關注的是可以賦予其真值“真”和“假”的語句。其目的是分析這些語句,無論是單獨的還是組合的。
命題邏輯 – 定義
命題是由宣告性語句組成的集合,具有真值“真”或真值“假”。命題由命題變數和連線片語成。我們用大寫字母(A、B 等)表示命題變數。連線詞連線命題變數。
下面給出一些命題的例子 −
- “人是凡人”,返回真值“真”
- “12 + 9 = 3 – 2”,返回真值“假”
以下不是命題 −
“A 小於 2”。這是因為除非我們給 A 一個特定的值,否則我們無法說這個語句是真還是假。
連線詞
在命題邏輯中,我們通常使用五種連線詞,它們是 −
或 ($\lor$)
與 ($\land$)
否定/非 ($\lnot$)
蘊含/如果-那麼 ($\rightarrow$)
當且僅當 ($\Leftrightarrow$)。
**或 ($\lor$)** − 兩個命題 A 和 B 的或運算(寫成 $A \lor B$)如果命題變數 A 或 B 中至少有一個為真,則為真。
真值表如下 −
| A | B | A ∨ B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 真 |
| 假 | 真 | 真 |
| 假 | 假 | 假 |
**與 ($\land$)** − 兩個命題 A 和 B 的與運算(寫成 $A \land B$)如果命題變數 A 和 B 都為真,則為真。
真值表如下 −
| A | B | A ∧ B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 假 |
| 假 | 真 | 假 |
| 假 | 假 | 假 |
**否定 ($\lnot$)** − 命題 A 的否定(寫成 $\lnot A$)在 A 為真時為假,在 A 為假時為真。
真值表如下 −
| A | ¬ A |
|---|---|
| 真 | 假 |
| 假 | 真 |
**蘊含/如果-那麼 ($\rightarrow$)** − 蘊含 $A \rightarrow B$ 是命題“如果 A,那麼 B”。如果 A 為真而 B 為假,則為假。其餘情況為真。
真值表如下 −
| A | B | A → B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 假 |
| 假 | 真 | 真 |
| 假 | 假 | 真 |
**當且僅當 ($ \Leftrightarrow $)** − $A \Leftrightarrow B$ 是雙條件邏輯連線詞,當 p 和 q 相同時為真,即兩者都為假或兩者都為真。
真值表如下 −
| A | B | A ⇔ B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 假 |
| 假 | 真 | 假 |
| 假 | 假 | 真 |
重言式
重言式是一個公式,對於其命題變數的每個值始終為真。
**示例** − 證明 $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ 是重言式
真值表如下 −
| A | B | A → B | (A → B) ∧ A | [( A → B ) ∧ A] → B |
|---|---|---|---|---|
| 真 | 真 | 真 | 真 | 真 |
| 真 | 假 | 假 | 假 | 真 |
| 假 | 真 | 真 | 假 | 真 |
| 假 | 假 | 真 | 假 | 真 |
正如我們所看到的,$\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ 的每個值都是“真”,它是一個重言式。
矛盾式
矛盾式是一個公式,對於其命題變數的每個值始終為假。
**示例** − 證明 $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ 是矛盾式
真值表如下 −
| A | B | A ∨ B | ¬ A | ¬ B | (¬ A) ∧ ( ¬ B) | (A ∨ B) ∧ [( ¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| 真 | 真 | 真 | 假 | 假 | 假 | 假 |
| 真 | 假 | 真 | 假 | 真 | 假 | 假 |
| 假 | 真 | 真 | 真 | 假 | 假 | 假 |
| 假 | 假 | 假 | 真 | 真 | 真 | 假 |
正如我們所看到的,$(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ 的每個值都是“假”,它是一個矛盾式。
偶然式
偶然式是一個公式,對於其命題變數的每個值,它既有一些真值,也有一些假值。
**示例** − 證明 $(A \lor B) \land (\lnot A)$ 是偶然式
真值表如下 −
| A | B | A ∨ B | ¬ A | (A ∨ B) ∧ (¬ A) |
|---|---|---|---|---|
| 真 | 真 | 真 | 假 | 假 |
| 真 | 假 | 真 | 假 | 假 |
| 假 | 真 | 真 | 真 | 真 |
| 假 | 假 | 假 | 真 | 假 |
正如我們所看到的,$(A \lor B) \land (\lnot A)$ 的每個值都既有“真”也有“假”,它是一個偶然式。
命題等價
如果滿足以下兩個條件中的任何一個,則兩個語句 X 和 Y 在邏輯上是等價的 −
每個語句的真值表具有相同的真值。
雙條件語句 $X \Leftrightarrow Y$ 是重言式。
**示例** − 證明 $\lnot (A \lor B)$ 和 $\lbrack (\lnot A) \land (\lnot B) \rbrack$ 是等價的
使用第一種方法(匹配真值表)進行測試
| A | B | A ∨ B | ¬ (A ∨ B) | ¬ A | ¬ B | [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| 真 | 真 | 真 | 假 | 假 | 假 | 假 |
| 真 | 假 | 真 | 假 | 假 | 真 | 假 |
| 假 | 真 | 真 | 假 | 真 | 假 | 假 |
| 假 | 假 | 假 | 真 | 真 | 真 | 真 |
在這裡,我們可以看到 $\lnot (A \lor B)$ 和 $\lbrack (\lnot A) \land (\lnot B) \rbrack$ 的真值相同,因此這兩個語句是等價的。
使用第二種方法(雙條件)進行測試
| A | B | ¬ (A ∨ B ) | [(¬ A) ∧ (¬ B)] | [¬ (A ∨ B)] ⇔ [(¬ A ) ∧ (¬ B)] |
|---|---|---|---|---|
| 真 | 真 | 假 | 假 | 真 |
| 真 | 假 | 假 | 假 | 真 |
| 假 | 真 | 假 | 假 | 真 |
| 假 | 假 | 真 | 真 | 真 |
由於 $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ 是重言式,因此這兩個語句是等價的。
逆命題、否命題和逆否命題
蘊含/如果-那麼 $(\rightarrow)$ 也稱為條件語句。它有兩個部分 −
- 假設,p
- 結論,q
如前所述,它表示為 $p \rightarrow q$。
**條件語句示例** − “如果你做作業,你就不會受到懲罰。”在這裡,“你做作業”是假設 p,“你不會受到懲罰”是結論 q。
**逆命題** − 條件語句的逆命題是對假設和結論的否定。如果語句是“如果 p,那麼 q”,則逆命題將是“如果非 p,那麼非 q”。因此,$p \rightarrow q$ 的逆命題是 $ \lnot p \rightarrow \lnot q$。
**示例** − “如果你做作業,你就不會受到懲罰”的逆命題是“如果你不做作業,你就會受到懲罰”。
**否命題** − 條件語句的否命題是透過交換假設和結論來計算的。如果語句是“如果 p,那麼 q”,則否命題將是“如果 q,那麼 p”。$p \rightarrow q$ 的否命題是 $q \rightarrow p$。
**示例** − “如果你做作業,你就不會受到懲罰”的否命題是“如果你不會受到懲罰,你就會做作業”。
**逆否命題** − 條件語句的逆否命題是透過交換逆命題的假設和結論來計算的。如果語句是“如果 p,那麼 q”,則逆否命題將是“如果非 q,那麼非 p”。$p \rightarrow q$ 的逆否命題是 $\lnot q \rightarrow \lnot p$。
**示例** − “如果你做作業,你就不會受到懲罰”的逆否命題是“如果你受到了懲罰,你就沒有做作業”。
對偶原理
對偶原理指出,對於任何真命題,透過將並集換成交集(反之亦然)並將全集換成空集(反之亦然)而獲得的對偶命題也是真的。如果任何語句的對偶是語句本身,則稱其為**自對偶**語句。
**示例** − $(A \cap B ) \cup C$ 的對偶是 $(A \cup B) \cap C$
正規化
我們可以將任何命題轉換為兩種正規化 −
- 合取正規化
- 析取正規化
合取正規化
如果一個複合語句是透過對用或連線的變數(包括變數的否定)進行與運算而獲得的,則它處於合取正規化。就集合運算而言,它是透過對用並集連線的變數進行交集運算而獲得的複合語句。
例子
$(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$
$(P \cup Q) \cap (Q \cup R)$
析取正規化
如果一個複合語句是透過對用與連線的變數(包括變數的否定)進行或運算而獲得的,則它處於析取正規化。就集合運算而言,它是透過對用交集連線的變數進行並集運算而獲得的複合語句。
例子
$(A \land B) \lor (A \land C) \lor (B \land C \land D)$
$(P \cap Q) \cup (Q \cap R)$
離散數學 - 謂詞邏輯
**謂詞邏輯**處理謂詞,謂詞是包含變數的命題。
謂詞邏輯 – 定義
謂詞是在某個特定域上定義的一個或多個變數的表示式。透過為變數賦值或對變數進行量化,可以將包含變數的謂詞轉換為命題。
以下是一些謂詞的例子 −
- 設 E(x, y) 表示“x = y”
- 設 X(a, b, c) 表示“a + b + c = 0”
- 設 M(x, y) 表示“x 與 y 結婚”
良構公式
良構公式 (wff) 是滿足以下任何條件的謂詞 −
所有命題常量和命題變數都是 wff
如果 x 是變數,Y 是 wff,則 $\forall x Y$ 和 $\exists x Y$ 也是 wff
真值和假值是 wff
每個原子公式都是 wff
連線 wff 的所有連線詞都是 wff
量詞
謂詞的變數由量詞量化。謂詞邏輯中有兩種型別的量詞 − 全稱量詞和存在量詞。
全稱量詞
全稱量詞指出其範圍內的語句對於特定變數的每個值都是正確的。它用符號 $\forall$ 表示。
$\forall x P(x)$ 讀作對於 x 的每個值,P(x) 都為真。
**示例** − “人是凡人”可以轉換為命題形式 $\forall x P(x)$,其中 P(x) 是表示 x 是凡人的謂詞,論域是所有男人。
存在量詞
存在量詞表示其作用範圍內的語句對於特定變數的某些值是正確的。它用符號$\exists$表示。
$\exists x P(x)$ 讀作:對於某些 x 值,P(x) 為真。
示例 − “有些人是不誠實的”可以轉化為命題形式$\exists x P(x)$,其中 P(x) 是表示 x 不誠實的謂詞,論域為某些人。
巢狀量詞
如果我們使用的量詞出現在另一個量詞的作用範圍內,則稱為巢狀量詞。
示例
$\forall\ a\: \exists b\: P (x, y)$,其中$P (a, b)$表示$a + b = 0$
$\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$,其中$P (a, b, c)$表示$a + (b + c) = (a + b) + c$
注意 − $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$
離散數學 - 推理規則
為了從我們已知其真值的語句中推匯出新的語句,使用推理規則。
推理規則是做什麼用的?
數學邏輯經常用於邏輯證明。證明是有效的論證,用於確定數學語句的真值。
論證是一系列語句。最後一個語句是結論,所有在其之前的語句都稱為前提(或假設)。符號“$\therefore$”(讀作因此)放在結論之前。有效論證是指結論遵循前提真值的論證。
推理規則為根據我們已有的語句構建有效論證提供模板或指導。
推理規則表
| 推理規則 | 名稱 | 推理規則 | 名稱 |
|---|---|---|---|
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$ |
附加 |
$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$ |
析取三段論 |
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$ |
合取 |
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$ |
假言三段論 |
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$ |
簡化 |
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$ |
構造性困境 |
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$ |
肯定前件 |
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$ |
破壞性困境 |
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$ |
否定後件 |
附加
如果 P 是前提,我們可以使用附加規則推匯出$P \lor Q$。
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$
示例
設 P 為命題,“他學習非常努力”為真。
因此 − “要麼他學習非常努力,要麼他是一個非常差的學生”。這裡 Q 是命題“他是一個非常差的學生”。
合取
如果 P 和 Q 是兩個前提,我們可以使用合取規則推匯出$P \land Q$。
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$
示例
設 P − “他學習非常努力”
設 Q − “他是班上最好的男孩”
因此 − “他學習非常努力,而且他是班上最好的男孩”。
簡化
如果$P \land Q$是一個前提,我們可以使用簡化規則推匯出 P。
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$
示例
“他學習非常努力,而且他是班上最好的男孩”,$P \land Q$
因此 − “他學習非常努力”。
肯定前件
如果 P 和$P \rightarrow Q$是兩個前提,我們可以使用肯定前件推匯出 Q。
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$
示例
“如果你有密碼,那麼你可以登入 Facebook”,$P \rightarrow Q$
“你有一個密碼”,P
因此 − “你可以登入 Facebook”。
否定後件
如果$P \rightarrow Q$和$\lnot Q$是兩個前提,我們可以使用否定後件推匯出$\lnot P$。
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$
示例
“如果你有密碼,那麼你可以登入 Facebook”,$P \rightarrow Q$
“你無法登入 Facebook”,$\lnot Q$
因此 − “你沒有密碼”。
析取三段論
如果$\lnot P$和$P \lor Q$是兩個前提,我們可以使用析取三段論推匯出 Q。
$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$
示例
“冰淇淋不是香草味的”,$\lnot P$
“冰淇淋要麼是香草味的,要麼是巧克力味的”,$P \lor Q$
因此 − “冰淇淋是巧克力味的”。
假言三段論
如果$P \rightarrow Q$和$Q \rightarrow R$是兩個前提,我們可以使用假言三段論推匯出$P \rightarrow R$。
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$
示例
“如果下雨,我就不去上學”,$P \rightarrow Q$
“如果我不去上學,我就不用做作業”,$Q \rightarrow R$
因此 − “如果下雨,我就不用做作業”。
構造性困境
如果$( P \rightarrow Q ) \land (R \rightarrow S)$和$P \lor R$是兩個前提,我們可以使用構造性困境推匯出$Q \lor S$。
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$
示例
“如果下雨,我就請假”,$( P \rightarrow Q )$
“如果外面很熱,我就去衝個澡”,$(R \rightarrow S)$
“要麼下雨,要麼外面很熱”,$P \lor R$
因此 − “我要麼請假,要麼去衝個澡”。
破壞性困境
如果$(P \rightarrow Q) \land (R \rightarrow S)$和$ \lnot Q \lor \lnot S $是兩個前提,我們可以使用破壞性困境推匯出$\lnot P \lor \lnot R$。
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$
示例
“如果下雨,我就請假”,$(P \rightarrow Q )$
“如果外面很熱,我就去衝個澡”,$(R \rightarrow S)$
“我要麼不請假,要麼不去沖澡”,$\lnot Q \lor \lnot S$
因此 − “要麼不下雨,要麼外面不熱”。
運算子與公理
群論是數學和抽象代數的一個分支,它定義了一種名為群的代數結構。一般來說,群包含一組元素和一個在該組上的任何兩個元素上的運算,以形成該組中的第三個元素。
1854年,英國數學家亞瑟·凱萊首次給出了群的現代定義:
“一組符號,它們彼此不同,並且任何兩個符號的乘積(無論順序如何),或任何一個符號自身的乘積,都屬於該集合,則稱該集合為一個群。這些符號通常不可交換[交換律],但具有結合律。”
在本章中,我們將瞭解構成集合論、群論和布林代數基礎的運算子和公理。
數學系統中的任何一組元素都可以用一組運算子和一些公理來定義。
在元素集合上定義的二元運算子是一個規則,它為每一對元素分配該集合中的唯一元素。例如,給定集合$ A = \lbrace 1, 2, 3, 4, 5 \rbrace $,如果它指定了根據對$(a,b)$查詢 c 的規則,使得$a,b,c \in A$,那麼我們可以說$\otimes$是運算$c = a \otimes b$的二元運算子。
數學系統的公理構成了可以從中推匯出規則的基本假設。公理是:
封閉性
如果對於集合中的每一對元素,運算子都能找到該集合中的唯一元素,則該集合對於二元運算子是封閉的。
示例
設$A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
這個集合在二元運算子乘法$(\ast)$下是封閉的,因為對於運算$c = a \ast b$,對於任何$a, b \in A$,乘積$c \in A$。
該集合在二元運算子除法$(\div)$下不是封閉的,因為對於運算$c = a \div b$,對於任何$a, b \in A$,乘積 c 可能不在集合 A 中。如果$a = 7, b = 2$,則$c = 3.5$。這裡$a,b \in A$但$c \notin A$。
結合律
集合 A 上的二元運算子$\otimes$在滿足以下性質時是結合的:
$(x \otimes y) \otimes z = x \otimes (y \otimes z)$,其中$x, y, z \in A $
示例
設$A = \lbrace 1, 2, 3, 4 \rbrace$
加法運算子$( + )$是結合的,因為對於任何三個元素$x,y,z \in A$,性質$(x + y) + z = x + ( y + z )$都成立。
減法運算子$( - )$不是結合的,因為
$$( x - y ) - z \ne x - ( y - z )$$
交換律
集合 A 上的二元運算子$\otimes$在滿足以下性質時是交換的:
$x \otimes y = y \otimes x$,其中$x, y \in A$
示例
設$A = \lbrace 1, 2, 3, 4 \rbrace$
加法運算子$( + )$是交換的,因為對於任何兩個元素$x,y \in A$,性質$x + y = y + x$都成立。
減法運算子$( - )$不是結合的,因為
$$x - y \ne y - x$$
分配律
集合 A 上的兩個二元運算子$\otimes$和$\circledast$在滿足以下性質時,$\otimes$對$\circledast$具有分配律:
$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$,其中$x, y, z \in A $
示例
設$A = \lbrace 1, 2, 3, 4 \rbrace$
乘法運算子$( * )$和加法運算子$( + )$對加法運算子 + 具有分配律,因為對於任何三個元素$x,y,z \in A$,性質$x * ( y + z ) = ( x * y ) + ( x * z )$都成立。
但是,這些運算子對乘法運算子$*$不具有分配律,因為
$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$
單位元
如果存在一個元素$e \in A$,使得滿足以下性質,則集合 A 對於 A 上的二元運算$\otimes$具有單位元:
$e \otimes x = x \otimes e$,其中$x \in A$
示例
設$Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
元素 1 是關於運算子$*$的單位元,因為對於任何元素$x \in Z$,
$$1 * x = x * 1$$
另一方面,減法運算$( - )$沒有單位元。
逆元
如果集合 A 關於二元運算子 $\otimes$ 有一個么元 $e$,那麼當且僅當對於集合 A 中的每一個元素 $x$,都存在另一個元素 $y \in A$,使得下列性質成立時,我們就說集合 A 有逆元。
$$x \otimes y = e$$
示例
令 $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$
給定加法運算 $(+)$ 和 $e = 0$,任何元素 x 的逆元是 $(-x)$,因為 $x + (-x) = 0$
德摩根律
德摩根律給出了兩個(或多個)集合的並集和交集與其補集之間的一對變換。這些定律是:
$$(A \cup B)' = A' \cap B'$$
$$(A \cap B)' = A' \cup B'$$
示例
令 $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$,以及
全集 $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$
$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$
$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$
$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$
$A \cap B = \lbrace 1, 3 \rbrace $
$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$
$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$
因此,我們可以看到 $(A \cup B)' = A' \cap B'$
$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
因此,我們可以看到 $(A \cap B)' = A' \cup B'$
離散數學 - 群論
半群
具有二元運算 $‘\omicron’$(複合運算)的有限或無限集合 $‘S’$ 稱為半群,如果它同時滿足以下兩個條件:
封閉性 - 對於每一個 $(a, b) \in S$,$(a \omicron b)$ 都必須存在於集合 S 中。
結合律 - 對於每一個元素 $a, b, c \in S$,$(a \omicron b) \omicron c = a \omicron (b \omicron c)$ 必須成立。
示例
具有加法運算的正整數集(不包括零)是一個半群。例如,$S = \lbrace 1, 2, 3, \dots \rbrace$
這裡封閉性成立,因為對於每一對 $(a, b) \in S$,$(a + b)$ 都存在於集合 S 中。例如,$1 + 2 = 3 \in S$
結合律也適用於每一個元素 $a, b, c \in S$,$(a + b) + c = a + (b + c)$。例如,$(1 + 2) + 3 = 1 + (2 + 3) = 6$
么半群
么半群是一個具有么元的半群。集合 S 的么元(用 $e$ 或 E 表示)是一個元素,使得對於 S 中的每一個元素 $a$,$(a \omicron e) = a$ 都成立。么元也稱為單位元。因此,么半群同時滿足三個性質:封閉性、結合律、么元。
示例
具有乘法運算的正整數集(不包括零)是一個么半群。$S = \lbrace 1, 2, 3, \dots \rbrace$
這裡封閉性成立,因為對於每一對 $(a, b) \in S$,$(a \times b)$ 都存在於集合 S 中。[例如,$1 \times 2 = 2 \in S$,等等]
結合律也適用於每一個元素 $a, b, c \in S$,$(a \times b) \times c = a \times (b \times c)$ [例如,$(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$,等等]
么元性質也適用於 S 中的每一個元素 $a$,$(a \times e) = a$ [例如,$(2 \times 1) = 2, (3 \times 1) = 3$,等等]。這裡的么元是 1。
群
群是一個具有逆元的么半群。集合 S 的逆元(用 I 表示)是一個元素,使得對於 S 中的每一個元素 $a$,$(a \omicron I) = (I \omicron a) = a$ 都成立。因此,群同時滿足四個性質:i) 封閉性,ii) 結合律,iii) 么元,iv) 逆元。群 G 的階是 G 中元素的數量,群中一個元素的階是最小的正整數 n,使得 $a^n$ 是該群 G 的么元。
例子
在矩陣乘法運算下,$N \times N$ 非奇異矩陣的集合構成一個群。
兩個 $N \times N$ 非奇異矩陣的乘積也是一個 $N \times N$ 非奇異矩陣,這滿足封閉性。
矩陣乘法本身是結合的。因此,結合律成立。
$N \times N$ 非奇異矩陣的集合包含單位矩陣,滿足么元性質。
由於所有矩陣都是非奇異的,它們都有逆元,這些逆元也是非奇異矩陣。因此,逆元性質也成立。
阿貝爾群
阿貝爾群 G 是一個群,對於 G 中的每一對元素 $(a, b)$,交換律都成立。因此,群同時滿足五個性質:i) 封閉性,ii) 結合律,iii) 么元,iv) 逆元,v) 交換律。
示例
具有加法運算的正整數集(包括零)是一個阿貝爾群。$G = \lbrace 0, 1, 2, 3, \dots \rbrace$
這裡封閉性成立,因為對於每一對 $(a, b) \in S$,$(a + b)$ 都存在於集合 S 中。[例如,$1 + 2 = 3 \in S$,等等]
結合律也適用於每一個元素 $a, b, c \in S$,$(a + b) + c = a + (b + c)$ [例如,$(1 + 2) + 3 = 1 + (2 + 3) = 6$,等等]
么元性質也適用於 S 中的每一個元素 $a$,$(a + e) = a$ [例如,$(2 + 0) = 2, (3 + 0) = 3$,等等]。這裡的么元是 0。
交換律也適用於 S 中的每一個元素 $a, b$,$(a + b) = (b + a)$ [例如,$(2 + 3) = (3 + 2) = 5$,等等]
迴圈群和子群
迴圈群是可以由單個元素生成的群。迴圈群的每一個元素都是某個特定元素的冪,這個特定元素稱為生成元。迴圈群可以由生成元'g'生成,使得群的每一個其他元素都可以寫成生成元'g'的冪。
示例
在乘法運算下,複數集 $\lbrace 1, -1, i, -i \rbrace$ 是一個迴圈群。
有兩個生成元:$i$ 和 $-i$,因為 $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$,以及 $(-i)^1 = -i, (-i)^2 = -1, (-i)^3 = i, (-i)^4 = 1$,涵蓋了群的所有元素。因此,它是一個迴圈群。
注意 - 迴圈群總是阿貝爾群,但並非所有阿貝爾群都是迴圈群。在加法運算下的有理數不是迴圈群,但它是阿貝爾群。
如果子群 H 是群 G 的一個子集(記作 $H ≤ G$),則它同時滿足四個性質:封閉性、結合律、么元和逆元。
群 G 的子群 H 如果不包含整個群 G,則稱為真子群(記作 $H < G$)。迴圈群的子群是迴圈群,阿貝爾群的子群也是阿貝爾群。
示例
令群 $G = \lbrace 1, i, -1, -i \rbrace$
則一些子群是 $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1, -1 \rbrace$,
這不是子群:$H_3 = \lbrace 1, i \rbrace$,因為 $(i)^{-1} = -i$ 不在 $H_3$ 中
偏序集 (POSET)
偏序集由一個集合和一個二元關係組成,該二元關係是自反的、反對稱的和傳遞的。“偏序集”縮寫為 POSET。
例子
在小於等於 $(\le)$ 二元運算下的實數集是一個偏序集。
令集合 $S = \lbrace 1, 2, 3 \rbrace$,運算子是 $\le$
關係將是 $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$
由於 $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$,此關係 R 是自反的
此關係 R 是反對稱的,因為
$\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R$ 且 $\lbrace (2, 1), (3, 1), (3, 2) \rbrace \notin R$
此關係 R 也是傳遞的,因為 $\lbrace (1, 2), (2, 3), (1, 3)\rbrace \in R$。
因此,它是一個偏序集。
在“可達性”運算下的有向無環圖的頂點集是一個偏序集。
哈斯圖
偏序集的哈斯圖是有向圖,其頂點是該偏序集的元素,弧覆蓋偏序集中的對 (x, y)。如果在偏序集中 $x < y$,則點 x 出現在哈斯圖中點 y 的下方。如果在偏序集中 $x < y < z$,則 x 和 z 之間的箭頭不會顯示,因為它是隱含的。
示例
$\lbrace 1, 2, 3 \rbrace$ 的子集的偏序集 $\lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ 由以下哈斯圖所示:
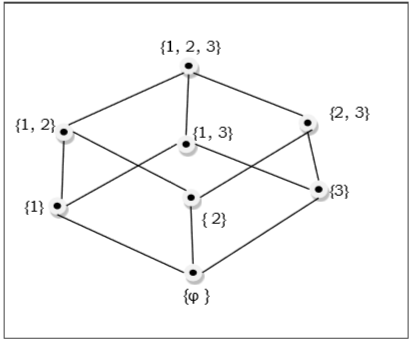
全序集
全序集或線性序集是一個偏序集,其中每一對元素都是可比較的。如果 $a \le b$ 或 $b \le a$ 成立,則元素 $a, b \in S$ 被稱為可比較的。三元性定律定義了這個全序集。全序集可以定義為一個分配格,它具有性質 $\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$,對於集合 S 中 a 和 b 的所有值都成立。
示例
由 $\subseteq$ 序的 $\lbrace a, b \rbrace$ 的冪集是一個全序集,因為冪集 $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b \rbrace \rbrace$ 的所有元素都是可比較的。
非全序集的例子
在運算 x 整除 y 下的集合 $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 不是全序集。
這裡,對於所有 $(x, y) \in S$,$x | y$ 都必須成立,但這不意味著 2 | 3,因為 2 不整除 3,或者 3 不整除 2。因此,它不是全序集。
格
格是一個偏序集 $(L, \le)$,對於其中的每一對 $\lbrace a, b \rbrace \in L$,都存在最小上界(記作 $a \lor b$)和最大下界(記作 $a \land b$)。LUB $(\lbrace a, b \rbrace)$ 稱為 a 和 b 的並。GLB $(\lbrace a, b \rbrace)$ 稱為 a 和 b 的交。
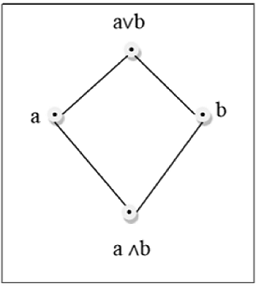
示例
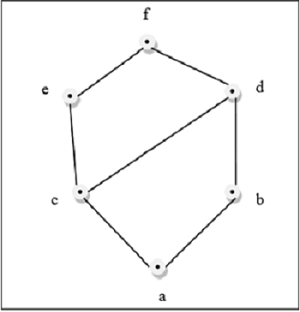
上圖是一個格,因為對於每一對 $\lbrace a, b \rbrace \in L$,都存在 GLB 和 LUB。
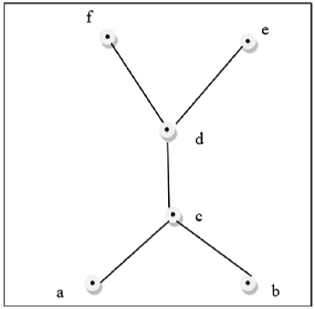
上圖不是格,因為GLB(a, b)和LUB(e, f)不存在。
下面討論其他一些格:
有界格
如果格L具有最大元1和最小元0,則L成為有界格。
補格
如果格L是有界格,並且格中的每個元素都有補元,則L成為補格。如果存在x’,滿足x∧x’=0且x∨x’=1,則元素x的補元為x’。
分配格
如果格滿足以下兩個分配律,則稱其為分配格。
a∨(b∧c) = (a∨b)∧(a∨c)
a∧(b∨c) = (a∧b)∨(a∧c)
模格
如果格滿足以下性質,則稱其為模格。
a∧(b∨(a∧d)) = (a∧b)∨(a∧d)
格的性質
冪等律
a∨a = a
a∧a = a
吸收律
a∨(a∧b) = a
a∧(a∨b) = a
交換律
a∨b = b∨a
a∧b = b∧a
結合律
a∨(b∨c) = (a∨b)∨c
a∧(b∧c) = (a∧b)∧c
格的對偶
格的對偶是透過互換'∨'和'∧'運算得到的。
示例
[a∨(b∧c)]的對偶是[a∧(b∨c)]
離散數學 - 計數理論
在日常生活中,很多時候需要找出一系列事件所有可能結果的數量。例如,從50名男性和38名女性中選出6名男性和4名女性組成的評審團有多少種方法?可以生成多少個不同的10位數的稅務識別號(PAN),使得前五位是大寫字母,接下來的四位是數字,最後一位又是大寫字母?為了解決這些問題,使用了數學計數理論。**計數**主要包括基本計數規則、排列規則和組合規則。
加法和乘法規則
**加法規則**和**乘法規則**用於將複雜的計數問題分解成簡單的子問題。
**加法規則** - 如果一系列任務T₁,T₂,…,Tₘ分別可以用w₁,w₂,…,wₘ種方式完成(條件是不能同時執行任務),那麼完成其中一項任務的方法數是w₁+w₂+…+wₘ。如果我們考慮兩個不相交的任務A和B(即A∩B=∅),那麼數學上|A∪B|=|A|+|B|。
**乘法規則** - 如果一系列任務T₁,T₂,…,Tₘ分別可以用w₁,w₂,…,wₘ種方式完成,並且每個任務都在前一個任務發生後到達,那麼完成這些任務的方法數為w₁×w₂×…×wₘ。數學上,如果任務B在任務A之後到達,那麼|A×B|=|A|×|B|。
示例
**問題** - 一個男孩住在X,想去Z學校。他必須先從家X到達Y,然後從Y到達Z。他可以乘坐3條公交路線或2條火車路線從X到Y。從那裡,他可以選擇4條公交路線或5條火車路線到達Z。從X到Z有多少種方法?
**解答** - 從X到Y,他可以有3+2=5種方法(加法規則)。然後,他可以用4+5=9種方法從Y到Z(加法規則)。因此,從X到Z,他可以用5×9=45種方法(乘法規則)。
排列
**排列**是某些元素的一種排列,其中順序很重要。換句話說,排列是元素的有序組合。
例子
從集合S={x, y, z}中每次取兩個元素,所有排列為:
xy, yx, xz, zx, yz, zy。
我們必須從數字集合S={1, 2, 3}中構成三位數的排列。當我們排列數字時,將形成不同的三位數。排列將是:123, 132, 213, 231, 312, 321。
排列數
從n個不同事物中取r個的排列數記為ⁿPᵣ
$$n_{P_{r}} = \frac{n!}{(n - r)!}$$
其中n!=1.2.3… (n-1).n
**證明** - 假設有n個不同的元素。
有n種方法填補第一個位置。填補第一個位置後,剩下(n-1)個元素。因此,有(n-1)種方法填補第二個位置。填補第一和第二個位置後,剩下(n-2)個元素。因此,有(n-2)種方法填補第三個位置。現在我們可以將填補第r個位置的方法數推廣為[n – (r–1)] = n–r+1
因此,從第一個位置到第r個位置的總方法數為:
ⁿPᵣ = n(n-1)(n-2)……(n-r+1)
=[n(n-1)(n-2)…(n-r+1)][(n-r)(n-r-1)…3.2.1]/[(n-r)(n-r-1)…3.2.1]
因此,
ⁿPᵣ = n!/(n-r)!
排列的一些重要公式
如果有n個元素,其中a₁個是某種型別的相同元素,a₂個是另一種型別的相同元素;a₃個是第三種類型的相同元素,以此類推,aᵣ個是第r種類型的相同元素,其中(a₁+a₂+…+aᵣ)=n。
那麼,這n個物件的排列數為= n! / [(a₁!)(a₂!)…(aᵣ!)]。
從n個不同元素中取n個元素的排列數= ⁿPₙ = n!
從n個不同元素中取r個元素的排列數,當x個特定事物總是佔據確定的位置= ⁿ⁻ˣPᵣ⁻ˣ
當r個指定事物總是放在一起時,n個不同元素的排列數為= r!(n−r+1)!
當r個指定事物從不放在一起時,n個不同元素的排列數為= n!–[r!(n−r+1)!]
從n個不同元素中取x個元素的環形排列數= ⁿPₓ/x
n個不同事物的環形排列數= ⁿPₙ/n
一些問題
**問題1** - 從一堆6張不同的卡片中,有多少種排列方法?
**解答** - 因為我們一次從6張卡片中取6張卡片,所以排列數為⁶P₆ = 6! = 720
**問題2** - 單詞'READER'的字母有多少種排列方法?
**解答** - 單詞'READER'有6個字母(2個E,1個A,1個D和2個R)。
排列數將是= 6! / [(2!)(1!)(1!)(2!)] = 180。
**問題3** - 單詞'ORANGE'的字母有多少種排列方法,使得子音只佔據偶數位置?
**解答** - 單詞'ORANGE'中有3個母音和3個子音。子音自身排列的方法數= ³P₃ = 3! = 6。剩下的3個空位將由3個母音以³P₃ = 3! = 6種方法填補。因此,排列總數為6 × 6 = 36
組合
**組合**是某些給定元素的選擇,其中順序無關緊要。
從n個事物中取r個的所有組合數為:
$$^nC_{r} = \frac{n!}{r!(n-r)!}$$
問題1
求集合{1, 2, 3, 4, 5, 6}中具有3個元素的子集的個數。
解答
集合的基數為6,我們必須從集合中選擇3個元素。這裡,順序無關緊要。因此,子集的個數為⁶C₃ = 20。
問題2
一個房間裡有6個男人和5個女人。從房間裡選擇3個男人和2個女人的方法有多少種?
解答
從6個男人中選擇3個男人的方法數為⁶C₃,從5個女人中選擇2個女人的方法數為⁵C₂。
因此,總方法數為:⁶C₃ × ⁵C₂ = 20 × 10 = 200
問題3
從總共9名學生中選擇3個不同的3人小組有多少種方法?
解答
讓我們將小組編號為1、2和3。
為第一個小組選擇3名學生的方法數:⁹C₃
在選擇第一個小組後,為第二個小組選擇3名學生的方法數:⁶C₃
在選擇第一個和第二個小組後,為第三個小組選擇3名學生的方法數:³C₃
因此,總方法數= ⁹C₃ × ⁶C₃ × ³C₃ = 84 × 20 × 1 = 1680
帕斯卡恆等式
帕斯卡恆等式,由布萊斯·帕斯卡在17世紀首次推匯出來,指出從n個元素中選擇k個元素的方法數等於從(n-1)個元素中選擇(k-1)個元素的方法數和從n-1個元素中選擇k個元素的方法數之和。
數學上,對於任何正整數k和n:ⁿCₖ = ⁿ⁻¹Cₖ₋₁ + ⁿ⁻¹Cₖ
**證明**:
$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$
= (n-1)! / [(k-1)!(n-k)!] + (n-1)! / [k!(n-k-1)!]
= (n-1)! (k / [k!(n-k)!] + (n-k) / [k!(n-k)!])
= (n-1)! n / [k!(n-k)!]
= n! / [k!(n-k)!]
= ⁿCₖ
鴿巢原理
1834年,德國數學家彼得·古斯塔夫·勒熱納·狄利克雷提出一個他稱之為抽屜原理的原理。現在,它被稱為鴿巢原理。
**鴿巢原理**指出,如果鴿巢的數量少於鴿子的總數,並且每隻鴿子都放在一個鴿巢中,那麼必須至少有一個鴿巢中有多於一隻鴿子。如果n只鴿子被放入m個鴿巢中,其中n>m,則至少有一個鴿巢中有多於一隻鴿子。
例子
十個人在一個房間裡互相握手。如果每個人至少握一次手,並且沒有人與同一個人握手多次,那麼有兩名參與握手的人握手的次數相同。
在一個30人的班級裡,至少有兩名學生的名字以相同的字母開頭。
容斥原理
容斥原理用於計算多個非互斥集合的並集的基數。對於兩個集合A和B,該原理指出:
$|A \cup B| = |A| + |B| - |A \cap B|$
對於三個集合A,B和C,該原理指出:
$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$
推廣公式:
$|\bigcup_{i=1}^{n}A_i|=\sum_{i=1}^{n}|A_i| - \sum\limits_{1\leq i<j\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\n-1}|A_1 \cap \dots \cap A_n|$
問題1
從1到50的整數中,有多少個是2或3的倍數,但不是兩者兼有的倍數?
解答
從1到50,有$50/2 = 25$個數是2的倍數。
有$50/3 = 16$個數是3的倍數。
有$50/6 = 8$個數是2和3的倍數。
所以,$|A|=25$,$|B|=16$,$|A \cap B|= 8$。
$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$
問題2
在一個50名學生的群體中,24人喜歡冷飲,36人喜歡熱飲,每個學生至少喜歡其中一種飲品。有多少人既喜歡咖啡又喜歡茶?
解答
設X為喜歡冷飲的學生集合,Y為喜歡熱飲的學生集合。
所以,$| X \cup Y | = 50$,$|X| = 24$,$|Y| = 36$
$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 10$
因此,有10名學生既喜歡茶又喜歡咖啡。
離散數學 - 機率
與計數概念密切相關的是機率。我們經常試圖猜測偶然事件的結果,例如紙牌遊戲、老虎機和彩票;也就是說,我們試圖找到獲得特定結果的可能性或機率。
機率可以被概念化為尋找事件發生的機會。從數學上講,它是對隨機過程及其結果的研究。機率定律廣泛應用於遺傳學、天氣預報、民意調查、股票市場等各種領域。
基本概念
機率論是由兩位17世紀的法國數學家布萊茲·帕斯卡和皮埃爾·德·費馬發明的,他們當時正在處理關於機會的數學問題。
在詳細介紹機率之前,讓我們先了解一些定義的概念。
隨機試驗- 在所有可能的結果已知且無法預先預測確切結果的實驗稱為隨機試驗。拋擲一枚公平的硬幣就是一個隨機試驗的例子。
樣本空間- 當我們進行實驗時,所有可能結果的集合S稱為樣本空間。如果我們拋擲一枚硬幣,樣本空間$S = \left \{ H, T \right \}$
事件- 樣本空間的任何子集都稱為事件。拋擲硬幣後,正面朝上就是一個事件。
“機率”一詞意味著特定事件發生的可能性。我們最多隻能說它們發生的可能性有多大,使用機率的概念。
$事件發生的機率 = \frac{有利結果的總數}{總結果數}$
由於任何事件的發生機率在0%到100%之間變化,因此機率在0到1之間變化。
計算機率的步驟
步驟1 - 計算實驗的所有可能結果。
步驟2 - 計算實驗的有利結果數。
步驟3 - 應用相應的機率公式。
拋擲硬幣
如果拋擲一枚硬幣,則有兩個可能的結果 - 正面$(H)$或反面$(T)$
所以,總結果數 = 2
因此,正面$(H)$朝上的機率為1/2,反面$(T)$朝上的機率為1/2
擲骰子
當擲骰子時,頂部可能出現六個結果 - $1, 2, 3, 4, 5, 6$。
任何一個數字的機率是1/6
得到偶數的機率是3/6 = 1/2
得到奇數的機率是3/6 = 1/2
從一副牌中抽取撲克牌
從一副52張牌中,如果抽取一張牌,求抽到A的機率,以及求抽到方塊的機率。
總可能結果數 - 52
抽到A的結果 - 4
抽到A的機率 = 4/52 = 1/13
抽到方塊的機率 = 13/52 = 1/4
機率公理
事件的機率始終在0到1之間變化。$[0 \leq P(x) \leq 1]$
對於不可能發生的事件,機率為0;對於必然發生的事件,機率為1。
如果一個事件的發生不受另一個事件的影響,則它們被稱為互斥事件或不相交事件。
如果$A_1, A_2....A_n$是互斥/不相交事件,則對於$i \ne j$,$P(A_i \cap A_j) = \emptyset $,並且$P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$
機率的性質
如果有兩個互補事件x和$\overline{x}$,則互補事件的機率為:
$$p(\overline{x}) = 1-p(x)$$
對於兩個非互斥事件A和B,兩個事件並集的機率:
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$
如果事件A是另一個事件B的子集(即$A \subset B$),則A的機率小於或等於B的機率。因此,$A \subset B$意味著$P(A) \leq p(B)$
條件機率
事件B的條件機率是在事件A已經發生的情況下事件B發生的機率。這寫成$P(B|A)$。
數學上 - $ P(B|A) = P(A \cap B)/ P(A)$
如果事件A和B是互斥的,則事件A之後事件B的條件機率將是事件B的機率,即$P(B)$。
問題1
在一個國家,所有青少年中有50%擁有腳踏車,所有青少年中有30%擁有腳踏車和腳踏車。如果青少年擁有腳踏車,那麼青少年擁有腳踏車的機率是多少?
解答
讓我們假設A是青少年只擁有腳踏車的事件,B是青少年只擁有腳踏車的事件。
所以,根據題目給出的問題,$P(A) = 50/100 = 0.5$,$P(A \cap B) = 30/100 = 0.3$。
$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$
因此,在青少年擁有腳踏車的情況下,青少年擁有腳踏車的機率為60%。
問題2
在一個班級中,所有學生中有50%玩板球,所有學生中有25%玩板球和排球。如果學生玩板球,那麼學生玩排球的機率是多少?
解答
讓我們假設A是學生只玩板球的事件,B是學生只玩排球的事件。
所以,根據題目給出的問題,$P(A) = 50/100 =0.5$,$P(A \cap B) = 25/ 100 =0.25$。
$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$
因此,如果學生玩板球,那麼學生玩排球的機率是50%。
問題3
有六臺好的筆記型電腦和三臺有缺陷的筆記型電腦混在一起。為了找到有缺陷的筆記型電腦,所有筆記型電腦都將隨機逐一測試。在前兩次挑選中找到兩臺有缺陷的筆記型電腦的機率是多少?
解答
設A為事件,我們在第一次測試中找到一臺有缺陷的筆記型電腦;B為事件,我們在第二次測試中找到一臺有缺陷的筆記型電腦。
因此,$P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$
貝葉斯定理
定理 - 如果A和B是兩個互斥事件,其中$P(A)$是A的機率,$P(B)$是B的機率,$P(A | B)$是在B為真的情況下A的機率,$P(B | A)$是在A為真的情況下B的機率,則貝葉斯定理指出:
$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$
貝葉斯定理的應用
在樣本空間的所有事件都是互斥事件的情況下。
在對於每個$A_i$,已知$P( A_i \cap B )$或已知$P( A_i )$和$P(B|A_i)$的情況下。
問題
考慮三個筆筒。第一個筆筒包含2支紅筆和3支藍筆;第二個筆筒有3支紅筆和2支藍筆;第三個筆筒有4支紅筆和1支藍筆。每個筆筒被選擇的機率相等。如果隨機抽取一支筆,那麼它是紅筆的機率是多少?
解答
設$A_i$為事件,即選擇第i個筆筒。
這裡,i = 1,2,3。
由於選擇筆筒的機率相等,$P(A_i) = 1/3$
設B為事件,即抽到一支紅筆。
在第一個筆筒的五支筆中選擇一支紅筆的機率為:
$P(B|A_1) = 2/5$
在第二個筆筒的五支筆中選擇一支紅筆的機率為:
$P(B|A_2) = 3/5$
在第三個筆筒的五支筆中選擇一支紅筆的機率為:
$P(B|A_3) = 4/5$
根據貝葉斯定理:
$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$
$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$
$= 3/5$
數學歸納法
數學歸納法是一種用於證明結果或為自然數建立陳述的技術。本部分透過各種示例說明此方法。
定義
數學歸納法是一種數學技術,用於證明某個陳述、公式或定理對於每個自然數都成立。
該技術包括兩個步驟來證明一個陳述,如下所示:
步驟1(基礎步驟) - 它證明該陳述對於初始值成立。
步驟2(歸納步驟) - 它證明如果該陳述對於第n次迭代(或數字n)成立,則它對於第(n+1)th次迭代(或數字n+1)也成立。
如何操作
步驟 1 − 考慮一個初始值,使得命題成立。需要證明該命題對於 n = 初始值成立。
步驟 2 − 假設該命題對於任意值 n = k 成立。然後證明該命題對於 n = k+1 成立。實際上,我們將 n = k+1 分成兩部分,一部分是 n = k(已證明),然後嘗試證明另一部分。
問題1
$3^n-1$ 是 2 的倍數,其中 n = 1, 2, ...
解答
步驟 1 − 對於 $n = 1, 3^1-1 = 3-1 = 2$,是 2 的倍數。
步驟 2 − 假設 $3^n-1$ 對於 $n=k$ 成立,因此,$3^k -1$ 成立(這是一個假設)
我們需要證明 $3^{k+1}-1$ 也是 2 的倍數。
$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$
第一部分 $(2 \times 3^k)$ 必定是 2 的倍數,第二部分 $(3^k -1)$ 根據之前的假設也成立。
因此,$3^{k+1} – 1$ 是 2 的倍數。
所以,已證明 $3^n – 1$ 是 2 的倍數。
問題2
$1 + 3 + 5 + ... + (2n-1) = n^2$,其中 $n = 1, 2, \dots $
解答
步驟 1 − 對於 $n=1, 1 = 1^2$,因此,步驟 1 成立。
步驟 2 − 假設該命題對於 $n=k$ 成立。
因此,$1 + 3 + 5 + \dots + (2k-1) = k^2$ 成立(這是一個假設)
我們需要證明 $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ 也成立。
$1 + 3 + 5 + \dots + (2(k+1) - 1)$
$= 1 + 3 + 5 + \dots + (2k+2 - 1)$
$= 1 + 3 + 5 + \dots + (2k + 1)$
$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$
$= k^2 + (2k + 1)$
$= (k + 1)^2$
所以,$1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ 成立,滿足步驟 2。
因此,已證明 $1 + 3 + 5 + \dots + (2n - 1) = n^2$。
問題3
證明 $(ab)^n = a^nb^n$ 對於任何自然數 n 都成立。
解答
步驟 1 − 對於 $n=1, (ab)^1 = a^1b^1 = ab$,因此,步驟 1 成立。
步驟 2 − 假設該命題對於 $n=k$ 成立,因此,$(ab)^k = a^kb^k$ 成立(這是一個假設)。
我們需要證明 $(ab)^{k+1} = a^{k+1}b^{k+1}$ 也成立。
已知,$(ab)^k = a^k b^k$
即, $(ab)^k (ab) = (a^k b^k ) (ab)$ [兩邊乘以 'ab']
即, $(ab)^{k+1} = (aa^k) ( bb^k)$
即, $(ab)^{k+1} = (a^{k+1}b^{k+1})$
因此,步驟 2 得證。
所以,$(ab)^n = a^nb^n$ 對於任何自然數 n 都成立。
強歸納法
強歸納法是數學歸納法的另一種形式。透過這種歸納技術,我們可以使用以下步驟證明命題函式 $P(n)$ 對於所有正整數 $n$ 都成立:
步驟 1(基礎步驟) − 證明初始命題 $P(1)$ 成立。
步驟 2(歸納步驟) − 證明條件語句 $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ 對於正整數 $k$ 成立。
離散數學 - 遞推關係
本章將討論遞迴技術如何推匯出序列並用於解決計數問題。以遞迴方式查詢序列項的過程稱為遞推關係。我們將學習線性遞推關係及其解的理論。最後,我們將介紹用於求解遞推關係的生成函式。
定義
遞推關係是一個遞迴定義序列的方程,其中下一項是前面各項的函式(將 $F_n$ 表示為 $i < n$ 的 $F_i$ 的某種組合)。
示例 − 斐波那契數列 − $F_n = F_{n-1} + F_{n-2}$,漢諾塔 − $F_n = 2F_{n-1} + 1$
線性遞推關係
k 次或 k 階線性遞推方程是一個遞推方程,其格式為 $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k}$($A_n$ 是常數,且 $A_k \neq 0$),它將數列表示為一階多項式。
以下是一些線性遞推方程的示例:
| 遞推關係 | 初始值 | 解 |
|---|---|---|
| Fn = Fn-1 + Fn-2 | a1 = a2 = 1 | 斐波那契數 |
| Fn = Fn-1 + Fn-2 | a1 = 1, a2 = 3 | 盧卡斯數 |
| Fn = Fn-2 + Fn-3 | a1 = a2 = a3 = 1 | 帕多萬數列 |
| Fn = 2Fn-1 + Fn-2 | a1 = 0, a2 = 1 | 佩爾數 |
如何求解線性遞推關係
假設,一個二階線性遞推關係為 − $F_n = AF_{n-1} +BF_{n-2}$,其中 A 和 B 為實數。
上述遞推關係的特徵方程為 −
$$x^2 - Ax - B = 0$$
求根時可能出現三種情況:
情況 1 − 如果該方程可分解為 $(x- x_1)(x- x_1) = 0$,併產生兩個不同的實根 $x_1$ 和 $x_2$,則 $F_n = ax_1^n+ bx_2^n$ 為解。[此處,a 和 b 為常數]
情況 2 − 如果該方程可分解為 $(x- x_1)^2 = 0$,併產生單個實根 $x_1$,則 $F_n = a x_1^n+ bn x_1^n$ 為解。
情況 3 − 如果該方程產生兩個不同的復根 $x_1$ 和 $x_2$,其極座標形式為 $x_1 = r \angle \theta$ 和 $x_2 = r \angle(- \theta)$,則 $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ 為解。
問題1
求解遞推關係 $F_n = 5F_{n-1} - 6F_{n-2}$,其中 $F_0 = 1$ 和 $F_1 = 4$
解答
遞推關係的特徵方程為 −
$$x^2 - 5x + 6 = 0,$$
所以 $(x - 3) (x - 2) = 0$
因此,根為 −
$x_1 = 3$ 和 $x_2 = 2$
根為實數且不相等。所以,這屬於情況 1。
因此,解為 −
$$F_n = ax_1^n + bx_2^n$$
此處,$F_n = a3^n + b2^n\ (因為\ x_1 = 3\ 且\ x_2 = 2)$
因此,
$1 = F_0 = a3^0 + b2^0 = a+b$
$4 = F_1 = a3^1 + b2^1 = 3a+2b$
求解這兩個方程,我們得到 $ a = 2$ 和 $b = -1$
因此,最終解為 −
$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$
問題2
求解遞推關係 − $F_n = 10F_{n-1} - 25F_{n-2}$,其中 $F_0 = 3$ 和 $F_1 = 17$
解答
遞推關係的特徵方程為 −
$$ x^2 - 10x -25 = 0$$
所以 $(x - 5)^2 = 0$
因此,存在單個實根 $x_1 = 5$
由於存在單個實數根,這屬於情況 2。
因此,解為 −
$F_n = ax_1^n + bnx_1^n$
$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$
$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$
求解這兩個方程,我們得到 $a = 3$ 和 $b = 2/5$
因此,最終解為 − $F_n = 3.5^n +( 2/5) .n.2^n $
問題3
求解遞推關係 $F_n = 2F_{n-1} - 2F_{n-2}$,其中 $F_0 = 1$ 和 $F_1 = 3$
解答
遞推關係的特徵方程為 −
$$x^2 -2x -2 = 0$$
因此,根為 −
$x_1 = 1 + i$ 和 $x_2 = 1 - i$
以極座標形式表示,
$x_1 = r \angle \theta$ 和 $x_2 = r \angle(- \theta)$,其中 $r = \sqrt 2$ 和 $\theta = \frac{\pi}{4}$
根為虛數。所以,這屬於情況 3。
因此,解為 −
$F_n = (\sqrt 2 )^n (a cos(n .\pi /4) + b sin(n .\pi /4))$
$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\pi /4) + b sin(0 .\pi /4) ) = a$
$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\pi /4) + b sin(1 . \pi /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$
求解這兩個方程,我們得到 $a = 1$ 和 $b = 2$
因此,最終解為 −
$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$
非齊次遞推關係和特解
如果遞推關係的形式為
$F_n = AF_{n-1} + BF_{n-2} + f(n)$,其中 $f(n) \ne 0$,則該遞推關係稱為非齊次遞推關係。
其相關的齊次遞推關係為 $F_n = AF_{n–1} + BF_{n-2}$
非齊次遞推關係的解 $(a_n)$ 包含兩部分。
第一部分是相關齊次遞推關係的解 $(a_h)$,第二部分是特解 $(a_t)$。
$$a_n=a_h+a_t$$
第一部分的解法在上一節中已討論。
為了找到特解,我們找到一個合適的試驗解。
令 $f(n) = cx^n$;令 $x^2 = Ax + B$ 為相關齊次遞推關係的特徵方程,並令 $x_1$ 和 $x_2$ 為其根。
如果 $x \ne x_1$ 且 $x \ne x_2$,則 $a_t = Ax^n$
如果 $x = x_1$,$x \ne x_2$,則 $a_t = Anx^n$
如果 $x = x_1 = x_2$,則 $a_t = An^2x^n$
示例
令非齊次遞推關係為 $F_n = AF_{n–1} + BF_{n-2} + f(n)$,其特徵根為 $x_1 = 2$ 和 $x_2 = 5$。對於 $f(n)$ 的不同可能值,試驗解如下: