
- 離散數學資源
- 離散數學 - 快速指南
- 離散數學 - 資源
- 離散數學 - 討論
離散數學 - 群論
半群
一個具有二元運算“ο”(複合)的有限或無限集合“S”稱為半群,如果它同時滿足以下兩個條件:-
封閉性 - 對於每個對 (a, b) ∈ S,(a ο b) 必須存在於集合 S 中。
結合律 - 對於每個元素 a, b, c ∈ S,(a ο b) ο c = a ο (b ο c) 必須成立。
示例
正整數集(不包括零)在加法運算下構成一個半群。例如,S = {1, 2, 3, …}
這裡封閉性成立,因為對於每個對 (a, b) ∈ S,(a + b) 都存在於集合 S 中。例如,1 + 2 = 3 ∈ S]
結合律也適用於每個元素 a, b, c ∈ S,(a + b) + c = a + (b + c)。例如,(1 + 2) + 3 = 1 + (2 + 3) = 5
么半群
么半群是一個具有單位元的半群。集合 S 的單位元(用 e 或 E 表示)是一個元素,使得對於每個元素 a ∈ S,(a ο e) = a。單位元也稱為單位元素。因此,么半群同時滿足三個性質:封閉性、結合律、單位元。
示例
正整數集(不包括零)在乘法運算下構成一個么半群。S = {1, 2, 3, …}
這裡封閉性成立,因為對於每個對 (a, b) ∈ S,(a × b) 都存在於集合 S 中。[例如,1 × 2 = 2 ∈ S,依此類推]
結合律也適用於每個元素 a, b, c ∈ S,(a × b) × c = a × (b × c) [例如,(1 × 2) × 3 = 1 × (2 × 3) = 6,依此類推]
單位元性質也適用於每個元素 a ∈ S,(a × e) = a [例如,(2 × 1) = 2,(3 × 1) = 3,依此類推]。這裡的單位元是 1。
群
群是一個具有逆元的么半群。集合 S 的逆元(用 I 表示)是一個元素,使得對於每個元素 a ∈ S,(a ο I) = (I ο a) = a。因此,群同時滿足四個性質:i) 封閉性,ii) 結合律,iii) 單位元,iv) 逆元。群 G 的階是 G 中元素的數量,群中元素的階是最小的正整數 n,使得 an 是該群 G 的單位元。
示例
N × N 非奇異矩陣集在矩陣乘法運算下構成一個群。
兩個 N × N 非奇異矩陣的乘積也是一個 N × N 非奇異矩陣,滿足封閉性。
矩陣乘法本身是結合的。因此,結合律成立。
N × N 非奇異矩陣集包含單位矩陣,滿足單位元性質。
由於所有矩陣都是非奇異的,因此它們都具有逆元,這些逆元也是非奇異矩陣。因此,逆元性質也成立。
阿貝爾群
阿貝爾群 G 是一個群,對於其中每個元素對 (a,b) ∈ G 都滿足交換律。因此,群同時滿足五個性質:i) 封閉性,ii) 結合律,iii) 單位元,iv) 逆元,v) 交換律。
示例
正整數集(包括零)在加法運算下構成一個阿貝爾群。G = {0, 1, 2, 3, …}
這裡封閉性成立,因為對於每個對 (a, b) ∈ S,(a + b) 都存在於集合 S 中。[例如,1 + 2 = 2 ∈ S,依此類推]
結合律也適用於每個元素 a, b, c ∈ S,(a + b) + c = a + (b + c) [例如,(1 +2) + 3 = 1 + (2 + 3) = 6,依此類推]
單位元性質也適用於每個元素 a ∈ S,(a × e) = a [例如,(2 × 1) = 2,(3 × 1) = 3,依此類推]。這裡的單位元是 1。
交換律也適用於每個元素 a ∈ S,(a × b) = (b × a) [例如,(2 × 3) = (3 × 2) = 3,依此類推]
迴圈群與子群
迴圈群是一個可以由單個元素生成的群。迴圈群的每個元素都是某個特定元素的冪,該元素稱為生成元。迴圈群可以由生成元“g”生成,使得該群的每個其他元素都可以寫成生成元“g”的冪。
示例
複數集 {1,-1, i, -i} 在乘法運算下構成一個迴圈群。
有兩個生成元:i 和 -i,因為 i1 = i,i2 = -1,i3 = -i,i4 = 1,以及 (-i)1 = -i,(-i)2 = -1,(-i)3 = i,(-i)4 = 1,涵蓋了群的所有元素。因此,它是一個迴圈群。
注意 - 迴圈群始終是阿貝爾群,但並非每個阿貝爾群都是迴圈群。有理數在加法運算下不是迴圈群,但它是阿貝爾群。
子群 H 是群 G 的子集(用 H ≤ G 表示),如果它同時滿足四個性質:封閉性、結合律、單位元和逆元。
群 G 的子群 H 不包含整個群 G 稱為真子群(用 H < G 表示)。迴圈群的子群是迴圈群,阿貝爾子群也是阿貝爾群。
示例
令群 G = {1, i, -1, -i}
則一些子群是 H1 = {1},H2 = {1,-1},
這不是子群:H3 = {1, i},因為 (i)-1 = -i 不在 H3 中
偏序集 (POSET)
偏序集由一個集合和一個二元關係組成,該關係是自反的、反對稱的和傳遞的。“偏序集”縮寫為 POSET。
示例
實數集在小於或等於 (≤) 的二元運算下構成一個偏序集。
令集合 S = {1, 2, 3},運算為 ≤
關係將是 {(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)}
此關係 R 是自反的,因為 {(1, 1), (2, 2), (3, 3)} ∈ R
此關係 R 是反對稱的,因為
{(1, 2), (1, 3), (2, 3)} ∈ R 和 {(1, 2), (1, 3), (2, 3)} ∉ R
此關係 R 也是傳遞的,因為 {(1,2), (2,3), (1,3)} ∈ R。
因此,它是一個偏序集。
有向無環圖的頂點集在“可達性”運算下構成一個偏序集。
哈斯圖
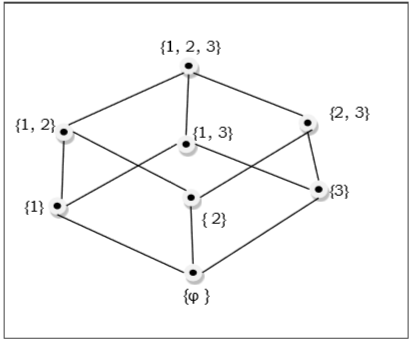
偏序集的哈斯圖是有向圖,其頂點是該偏序集的元素,弧覆蓋偏序集中的對 (x, y)。如果在偏序集中 x < y,則點 x 在哈斯圖中出現在點 y 的下方。如果在偏序集中 x {1, 2, 3} 的子集的偏序集 = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}} 由以下哈斯圖表示:- 線性序集或全序集是偏序集,其中每對元素都是可比較的。如果元素 a, b ∈ S 滿足 a ≤ b 或 b ≤ a,則稱元素 a, b ∈ S 是可比較的。三等分律定義了這個全序集。全序集可以定義為一個分配格,它具有屬性 {a ∨ b, a ∧ b} = {a, b},對於集合 S 中的所有 a 和 b 值。 {a, b} 的冪集按 ⊆ 排序是一個全序集,因為冪集 P = {∅, {a}, {b}, {a, b}} 的所有元素都是可比較的。 集合 S = {1, 2, 3, 4, 5, 6} 在運算 x 整除 y 下不是一個全序集。 這裡,對於所有 (x, y) ∈ S,x | y 必須成立,但 2 | 3 不成立,因為 2 不整除 3 或 3 不整除 2。因此,它不是一個全序集。 格是一個偏序集 (L, ≤),對於其中每對 {a, b} ∈ L 都有一個最小上界(用 a ∨ b 表示)和一個最大下界(用 a ∧ b 表示)。LUB ({a,b}) 稱為 a 和 b 的並。GLB ({a,b}) 稱為 a 和 b 的交。 上圖是一個格,因為對於每對 {a, b} ∈ L,都存在 GLB 和 LUB。 上圖不是一個格,因為 GLB (a, b) 和 LUB (e, f) 不存在。 下面討論其他一些格:- 如果格 L 具有最大元素 1 和最小元素 0,則它成為有界格。 如果格 L 是有界格,並且如果格中的每個元素都有一個補元,則它成為補格。如果存在 x(x ∧ x'=0 且 x ∨ x' = 1),則元素 x 具有補元 x' 如果格滿足以下兩個分配性質,則稱為分配格。 a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c) 如果格滿足以下性質,則稱為模格。 a ∧( b ∨ (a ∧ d)) = (a ∧ b) ∨ (a ∧ d) a ∨ a = a a ∧ a = a a ∨ (a ∧ b) = a a ∧ (a ∨ b) = a示例
線性序集
示例
非全序集的示例
格
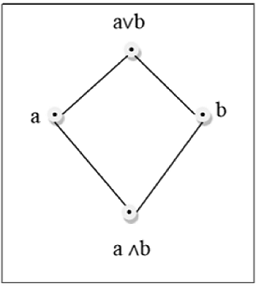
示例
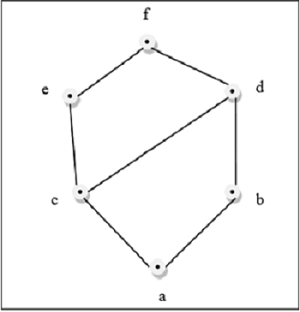
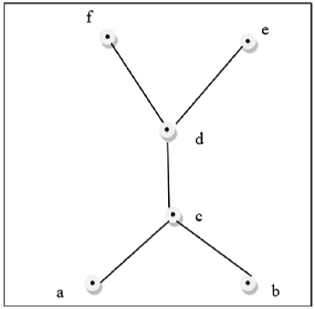
有界格
補格
分配格
模格
格的性質
冪等律
吸收律
交換律
$a \lor b = b \lor a$
$a \land b = b \land a$
結合律(Associative Properties)
$a \lor (b \lor c) = (a \lor b) \lor c$
$a \land (b \land c) = (a \land b) \land c$
格的對偶(Dual of a Lattice)
格的對偶是透過交換“$\lor$”和“$\land$”運算得到的。
示例
$\lbrack a \lor (b \land c) \rbrack$ 的對偶是 $\lbrack a \land (b \lor c) \rbrack$