離散數學 - 集合

上一頁
下一頁

德國數學家G. 康托爾引入了集合的概念。他將集合定義為根據某些規則或描述選擇的明確且可區分物件的集合。

集合理論構成了其他幾個研究領域的基礎，例如計數理論、關係、圖論和有限狀態機。在本章中，我們將介紹集合論的不同方面。

集合 - 定義

集合是不同元素的無序集合。可以使用集合括號列出其元素來顯式地寫出集合。如果元素的順序改變或集合的任何元素重複，則不會對集合產生任何變化。

集合的一些例子

  • 所有正整數的集合
  • 太陽系中所有行星的集合
  • 印度所有邦的集合
  • 所有小寫字母的集合

集合的表示

集合可以用兩種方式表示：

  • 列舉法或表格法
  • 集合構造器表示法

列舉法或表格法

集合透過列出構成它的所有元素來表示。元素用大括號括起來，並用逗號分隔。

例1 - 英文字母表中的母音集合，$A = \lbrace a,e,i,o,u \rbrace$

例2 - 小於10的奇數集合，$B = \lbrace 1,3,5,7,9 \rbrace$

集合構造器表示法

集合透過指定集合元素共有的屬性來定義。集合描述為$A = \lbrace x : p(x) \rbrace$

例1 - 集合$\lbrace a,e,i,o,u \rbrace$ 寫作：

$A = \lbrace x : \text{x是英文字母表中的母音} \rbrace$

例2 - 集合$\lbrace 1,3,5,7,9 \rbrace$ 寫作：

$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$

如果元素x是集合S的成員，則表示為$x \in S$；如果元素y不是集合S的成員，則表示為$y \notin S$。

例 - 如果 $S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ 但 $1.5 \notin S$

一些重要的集合

N - 所有自然數的集合 = $\lbrace1, 2, 3, 4, .....\rbrace$

Z - 所有整數的集合 = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$

Z+ - 所有正整數的集合

Q - 所有有理數的集合

R - 所有實數的集合

W - 所有整數的集合

集合的基數

集合S的基數，記為$|S|$，是集合的元素個數。這個數也稱為基數。如果一個集合有無限多個元素，則它的基數是$\infty$。

例 - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$

如果有兩個集合X和Y，

  • $|X| = |Y|$ 表示兩個集合X和Y具有相同的基數。當X中的元素個數恰好等於Y中的元素個數時，就會發生這種情況。在這種情況下，存在一個從X到Y的雙射函式“f”。

  • $|X| \le |Y|$ 表示集合X的基數小於或等於集合Y的基數。當X中的元素個數小於或等於Y中的元素個數時，就會發生這種情況。這裡，存在一個從X到Y的單射函式“f”。

  • $|X| \lt |Y|$ 表示集合X的基數小於集合Y的基數。當X中的元素個數小於Y中的元素個數時，就會發生這種情況。這裡，從X到Y的函式“f”是單射函式，但不是雙射函式。

  • $如果\ |X| \le |Y| 且 |X| \ge |Y|，則 |X| = |Y|。集合X和Y通常被稱為等價集合。

集合的型別

集合可以分為許多型別。其中一些是有限的、無限的、子集、全集、真子集、單元素集等等。

有限集

包含一定數量元素的集合稱為有限集。

例 - $S = \lbrace x \:| \:x \in N$ 且 $70 \gt x \gt 50 \rbrace$

無限集

包含無限多個元素的集合稱為無限集。

例 - $S = \lbrace x \: | \: x \in N $ 且 $ x \gt 10 \rbrace$

子集

如果集合X的每個元素都是集合Y的元素，則集合X是集合Y的子集（寫成$X \subseteq Y$）。

例1 - 令，$X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 且 $Y = \lbrace 1, 2 \rbrace$。這裡集合Y是集合X的子集，因為集合Y的所有元素都在集合X中。因此，我們可以寫成$Y \subseteq X$。

例2 - 令，$X = \lbrace 1, 2, 3 \rbrace$ 且 $Y = \lbrace 1, 2, 3 \rbrace$。這裡集合Y是集合X的子集（不是真子集），因為集合Y的所有元素都在集合X中。因此，我們可以寫成$Y \subseteq X$。

真子集

“真子集”可以定義為“子集但不等於”。如果集合X的每個元素都是集合Y的元素，且$|X| \lt |Y|$，則集合X是集合Y的真子集（寫成$ X \subset Y $）。

例 - 令，$X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ 且 $Y = \lbrace 1, 2 \rbrace$。這裡集合$Y \subset X$，因為Y中的所有元素也包含在X中，並且X至少比集合Y多一個元素。

全集

它是特定上下文或應用中所有元素的集合。該上下文或應用中的所有集合本質上都是這個全集的子集。全集表示為$U$。

例 - 我們可以將$U$定義為地球上所有動物的集合。在這種情況下，所有哺乳動物的集合是$U$的子集，所有魚類的集合是$U$的子集，所有昆蟲的集合是$U$的子集，等等。

空集或空集

空集不包含任何元素。它表示為$\emptyset$。由於空集中的元素數量是有限的，因此空集是有限集。空集或空集的基數為零。

例 - $S = \lbrace x \:| \: x \in N$ 且 $7 \lt x \lt 8 \rbrace = \emptyset$

單元素集或單元集

單元素集或單元集只包含一個元素。單元素集表示為$\lbrace s \rbrace$。

例 - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$

相等集

如果兩個集合包含相同的元素，則稱它們相等。

例 - 如果$A = \lbrace 1, 2, 6 \rbrace$ 且 $B = \lbrace 6, 1, 2 \rbrace$，則它們相等，因為集合A的每個元素都是集合B的元素，集合B的每個元素都是集合A的元素。

等價集

如果兩個集合的基數相同，則它們稱為等價集合。

例 - 如果$A = \lbrace 1, 2, 6 \rbrace$ 且 $B = \lbrace 16, 17, 22 \rbrace$，則它們是等價的，因為A的基數等於B的基數。即$|A| = |B| = 3$

重疊集

至少有一個公共元素的兩個集合稱為重疊集。

對於重疊集：

  • $n(A \cup B) = n(A) + n(B) - n(A \cap B)$

  • $n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$

  • $n(A) = n(A - B) + n(A \cap B)$

  • $n(B) = n(B - A) + n(A \cap B)$

例 - 令，$A = \lbrace 1, 2, 6 \rbrace$ 且 $B = \lbrace 6, 12, 42 \rbrace$。有一個公共元素“6”，因此這些集合是重疊集。

不相交集

如果兩個集合A和B沒有任何公共元素，則它們稱為不相交集。因此，不相交集具有以下性質：

  • $n(A \cap B) = \emptyset$

  • $n(A \cup B) = n(A) + n(B)$

例 - 令，$A = \lbrace 1, 2, 6 \rbrace$ 且 $B = \lbrace 7, 9, 14 \rbrace$，沒有一個公共元素，因此這些集合是重疊集。（此處原文有誤，應為不相交集）

文氏圖

文氏圖由約翰·文恩於1880年發明，是一種示意圖，顯示不同數學集合之間所有可能的邏輯關係。

例子

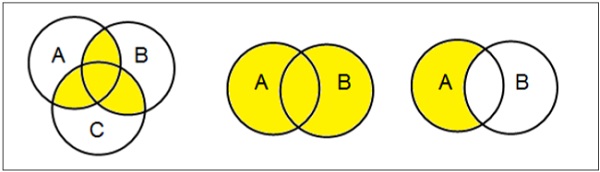
Venn Diagram

集合運算

集合運算包括集合並、集合交、集合差、集合補和笛卡爾積。

集合並

集合A和B的並集（記作$A \cup B$）是屬於A、屬於B或同時屬於A和B的元素的集合。因此，$A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$。

例 - 如果$A = \lbrace 10, 11, 12, 13 \rbrace$ 且 B = $\lbrace 13, 14, 15 \rbrace$，則$A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$。（公共元素只出現一次）

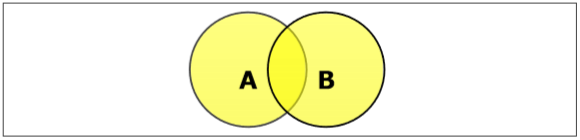
Set Union

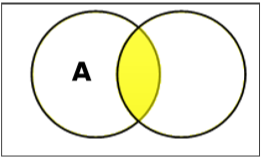
集合交

集合A和B的交集（記作$A \cap B$）是同時屬於A和B的元素的集合。因此，$A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$。

例 - 如果$A = \lbrace 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$，則$A \cap B = \lbrace 13 \rbrace$。

Set Intersection

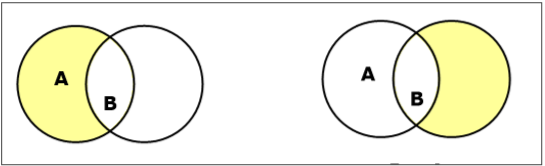
集合差/相對補集

集合A和B的集合差（記作$A – B$）是隻屬於A而不屬於B的元素的集合。因此，$A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$。

例 - 如果$A = \lbrace 10, 11, 12, 13 \rbrace$ 且 $B = \lbrace 13, 14, 15 \rbrace$，則$(A - B) = \lbrace 10, 11, 12 \rbrace$ 且 $(B - A) = \lbrace 14, 15 \rbrace$。這裡，我們可以看到$(A - B) \ne (B - A)$

Set Difference

集合的補集

集合A的補集（記作$A’$）是不屬於集合A的元素的集合。因此，$A' = \lbrace x | x \notin A \rbrace$。

更具體地說，$A'= (U - A)$，其中$U$是包含所有物件的全集。

例 - 如果$A = \lbrace x \:| \: x\ \: {屬於奇數集合} \rbrace$，則$A' = \lbrace y\: | \: y\ \: {不屬於奇數集合} \rbrace$

Complement Set

笛卡爾積/叉積

n個集合$A_1, A_2, \dots A_n$的笛卡爾積記作$A_1 \times A_2 \dots \times A_n$，可以定義為所有可能的序對$(x_1, x_2, \dots x_n)$，其中$x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$

例 - 如果我們取兩個集合$A = \lbrace a, b \rbrace$ 且 $B = \lbrace 1, 2 \rbrace$，

集合 A 和 B 的笛卡爾積記作 − $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$

集合 B 和 A 的笛卡爾積記作 − $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$

冪集

集合 S 的冪集是 S 的所有子集（包括空集）的集合。集合 S 的基數為 n，則其冪集的基數為 $2^n$。冪集記作 $P(S)$。

示例 −

對於集合 $S = \lbrace a, b, c, d \rbrace$，讓我們計算其子集 −

  • 包含 0 個元素的子集 − $\lbrace \emptyset \rbrace$（空集）

  • 包含 1 個元素的子集 − $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$

  • 包含 2 個元素的子集 − $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$

  • 包含 3 個元素的子集 − $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$

  • 包含 4 個元素的子集 − $\lbrace a, b, c, d \rbrace$

因此，$P(S)=$

$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$

$| P(S) | = 2^4 = 16$

注意 − 空集的冪集也是空集。

$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$

集合的劃分

集合 S 的劃分是由 n 個不相交子集 $P_1, P_2, \dots P_n$ 組成的集合，滿足以下三個條件 −

  • $P_i$ 不包含空集。

    $\lbrack P_i \ne \lbrace \emptyset \rbrace\ \forall\ 0 \lt i \le n \rbrack$

  • 這些子集的並集必須等於整個原集合。

    $\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$

  • 任意兩個不同子集的交集為空集。

    $\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ \forall\ a \ne b\ 且\ n \ge a,\: b \ge 0 \rbrack$

示例

設 $S = \lbrace a, b, c, d, e, f, g, h \rbrace$

一種可能的劃分是 $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$

另一種可能的劃分是 $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$

貝爾數

貝爾數給出了劃分集合的方法數。它們用 $B_n$ 表示，其中 n 是集合的基數。

示例 −

設 $S = \lbrace 1, 2, 3\rbrace$，$n = |S| = 3$

不同的劃分有 −

1. $\emptyset , \lbrace 1, 2, 3 \rbrace$

2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$

3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$

4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$

5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$

因此 $B_3 = 5$

列印頁面
上一頁
下一頁
廣告
© . All rights reserved.