採用圖解法,判斷下列方程組是否相容。如果相容,則求解。
\( 3 x+y+4=0 \)
\( 6 x-2 y+4=0 \)
解題步驟
我們需要判斷給定的線性方程組是否相容/不相容。如果相容,則用圖形法求解。
解答
(i) $3x+y+4=0$.........(i)
$6x-2y+4=0$.........(ii)
這裡,
$a_{1}=3, b_{1}=1, c_{1}=4$
$a_{2}=6, b_{2}=-2, c_{2}=4$
$\frac{a_{1}}{a_{2}}=\frac{3}{6}$
$=\frac{1}{2}$
$\frac{b_{1}}{b_{2}}=\frac{1}{-2}$
$\frac{c_{1}}{c_{2}}=\frac{4}{4}$
$=1$
$\frac{a_{1}}{a_{2}} ≠ \frac{b_{1}}{b_{2}}$
這意味著,
給定的方程組相容。
對於方程 (i),
$y=-4-3x$
| $x$ | 0 | $-1$ |
| $y$ | $-4$ | $-1$ |
在座標系上繪製點 $( 0,\ -4)$ 和 $(-1,\ -1)$,並連線它們得到方程 $3x+y+4=0$ 的影像。
$3x+y+4=0$
對於方程 (ii),
$2y=6x+4$
$y=3x+2$
| $x$ | $-1$ | 0 |
| $y$ | $-1$ | 2 |
在座標系上繪製點 $(-1,\ -1)$ 和 $( 0,\ 2)$,並連線它們得到方程 $6x-2y+4=0$ 的影像。
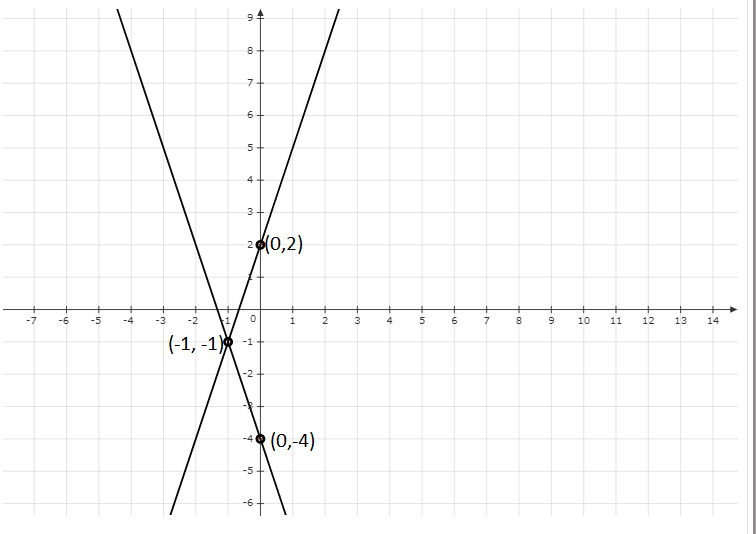
$x=-1,\ y=-1$ 是給定方程組的解。因此,該方程組相容。
(ii) $x-2y-6=0$.........(i)
$3x-6y=0$.........(ii)
這裡,
$a_{1}=1, b_{1}=-2, c_{1}=-6$
$a_{2}=3, b_{2}=-6, c_{2}=0$
$\frac{a_{1}}{a_{2}}=\frac{1}{3}$
$\frac{b_{1}}{b_{2}}=\frac{-2}{-6}$
$=\frac{1}{3}$
$\frac{c_{1}}{c_{2}}=\frac{-6}{0}$
$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}≠\frac{c_{1}}{c_{2}}$
這意味著,
由給定方程表示的直線平行。
因此,給定的方程組不相容。
(iii) $x+y-3=0$.........(i)
$3x+3y-9=0$.........(ii)
這裡,
$a_{1}=1, b_{1}=1, c_{1}=-3$
$a_{2}=3, b_{2}=3, c_{2}=-9$
$\frac{a_{1}}{a_{2}}=\frac{1}{3}$
$\frac{b_{1}}{b_{2}}=\frac{1}{3}$
$\frac{c_{1}}{c_{2}}=\frac{-3}{-9}$
$=\frac{1}{3}$
$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_1}{c_2}$
這意味著,
給定的方程組是重合的,因此是相容的。
對於方程 (i),
$y=3-x$
| $x$ | 0 | $3$ |
| $y$ | $3$ | $0$ |
在座標系上繪製點 $( 0,\ 3)$ 和 $(3,\ 0)$,並連線它們得到方程 $x+y=3$ 的影像。
對於方程 (ii),
$3y=9-3x$
$y=3-x$
| $x$ | $0$ | 3 |
| $y$ | $3$ | 0 |
在座標系上繪製點 $(0,\ 3)$ 和 $(3,\ 0)$,並連線它們得到方程 $3x+3y=9$ 的影像。
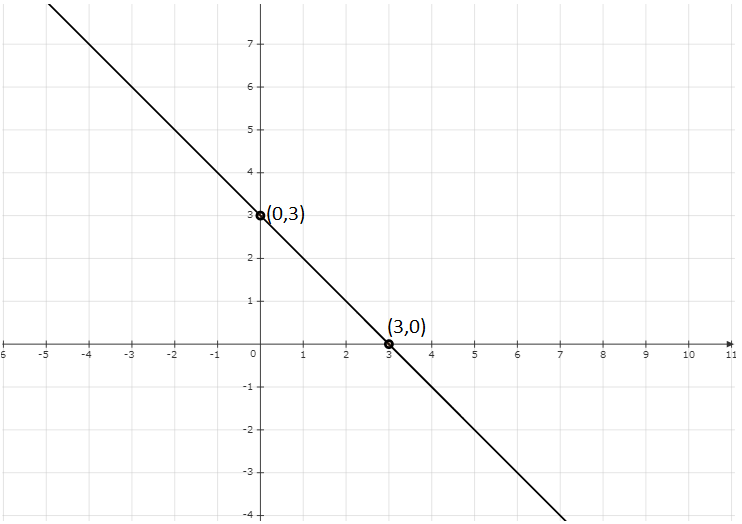
由於直線重合,所以有無窮多個解。


 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP