資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究從海平面上一座高 75 米的燈塔頂端觀察，兩艘船的俯角分別為 30° 和 45°。如果一艘船正好在另一艘船的後面，並且都在燈塔的同一側，求這兩艘船之間的距離。
已知
從一棟 \( 75 \mathrm{~m} \) 高的燈塔頂端觀察，兩艘船的俯角分別為 \( 30^{\circ} \) 和 \( 45^{\circ} \)。
一艘船正好在另一艘船的後面，並且都在燈塔的同一側。
要求
我們需要求出這兩艘船之間的距離。
解：
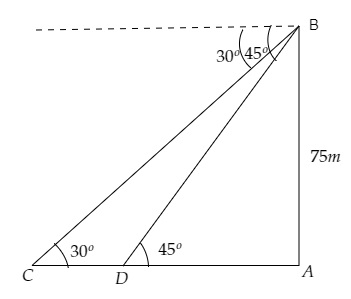
設 $AB$ 為高燈塔的高度，$C, D$ 為兩艘船，一艘在另一艘的後面。
從圖中，
$\mathrm{AB}=75 \mathrm{~m}, \angle \mathrm{BCA}=30^{\circ}, \angle \mathrm{BDA}=45^{\circ}$
設船 $D$ 與燈塔之間的距離為 $\mathrm{DA}=x \mathrm{~m}$，兩艘船之間的距離為 $\mathrm{CD}=y \mathrm{~m}$。
這意味著，
$\mathrm{CA}=x+y \mathrm{~m}$
我們知道，
$\tan \theta=\frac{\text { 對邊 }}{\text { 鄰邊 }}$
$=\frac{\text { AB }}{DA}$
$\Rightarrow \tan 45^{\circ}=\frac{75}{x}$
$\Rightarrow 1=\frac{75}{x}$
$\Rightarrow x=75 \mathrm{~m}$.........(i)
類似地，
$\tan \theta=\frac{\text { 對邊 }}{\text { 鄰邊 }}$
$=\frac{\text { BA }}{CA}$
$\Rightarrow \tan 30^{\circ}=\frac{75}{x+y}$
$\Rightarrow \frac{1}{\sqrt3}=\frac{75}{75+y}$ [由 (i) 得]
$\Rightarrow 75+y=75\sqrt3 \mathrm{~m}$
$\Rightarrow y=75(\sqrt3-1) \mathrm{~m}$
因此，兩艘船之間的距離為 $75(\sqrt3-1) \mathrm{~m}$。
76 次瀏覽
