圓形扇形的面積

---

介紹

圓形扇形的面積是指扇形邊界內包圍的面積大小。在本教程中，我們將學習圓形扇形以及如何計算圓形扇形的面積。

圓形扇形的面積是指扇形邊界內包圍的面積大小。

扇形總是從圓心開始。扇形的面積定義為圓內由兩條半徑及其相鄰弧線所圍成的部分。半圓是圓中最常見的扇形，它代表半個圓。在本文的後續部分，我們將學習更多關於面積、面積公式以及如何使用弧度和角度計算扇形面積的內容。

我們還將透過一些例子來更好地理解這些主題。

圓形扇形

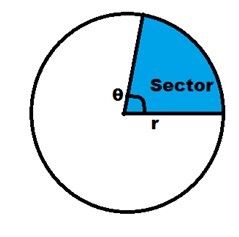
扇形被認為是圓的一部分，它有兩條半徑和一條弧。圓被分成兩個扇形，一個叫小扇形，另一個叫大扇形。小扇形是圓形較小的一部分，大扇形是圓形較大的部分。

圓形扇形的面積

• 使用扇形面積公式來計算扇形包圍的總面積。扇形的面積可以使用以下公式計算：

  $$\mathrm{扇形面積 =\frac{θ}{360^\circ} × πr^2}$$

  其中 θ 是圓心角（以度為單位），r 是圓的半徑。

• 圓形扇形面積 =$\mathrm{\frac{1}{2} × r^2 θ }$，其中 θ 是圓心角（以弧度為單位），r 是圓的半徑。

• 讓我們推匯出圓形扇形面積的公式。我們知道一個完整的圓是 360 度。圓心角為 360° 的圓的面積為 πr²，其中 r 是圓的半徑。

• 如果圓心角為 1°，則扇形的面積為 $\mathrm{\frac{ πr^2}{360°}}$。因此，如果圓心角為 θ，則扇形的面積 =$\mathrm{=(\frac{θ}{360°})\times πr^2}$，其中 θ 是圓心角（以度為單位），r 是圓的半徑。

• 換句話說，πr² 表示整個圓的面積，而 $\mathrm{\frac{θ}{360°}}$ 表示扇形覆蓋了圓的多少比例。

扇形公式

如果圓心角 θ 以弧度表示，則

$$\mathrm{扇形面積 = \frac{1}{2} × r^2 θ,}$$

其中 θ 是圓心角（以弧度為單位），r 是圓的半徑。

需要注意的是，半圓和象限是特殊的扇形，其角度分別為 180° 和 90°。

例題

1) 半徑為 6，圓心角為 60° 的圓形扇形的面積是多少？

答：扇形的面積$\mathrm{=(\frac{θ}{360°}) × πr^2=(\frac{60°}{360°}) × π.6^2=6π}$

因此，面積是 6π。

2) 半徑為 5，圓心角為 120° 的圓形扇形的面積是多少？

答：扇形的面積$\mathrm{=(\frac{θ}{360°}) × πr^2=(\frac{120°}{360°}) × π.5^2=8.3π}$

因此，面積是 8.3π。

結論

在本教程中，我們學習了圓形扇形及其面積的計算。扇形表示圓的一部分的面積。我們知道圓的面積用公式 πr² 計算。我們知道一個完整的圓是 360 度。圓心角為 360° 的圓的面積為 πr²，其中 r 是圓的半徑。如果圓心角為 1°，則面積為 $\mathrm{\frac{πr^2}{360°}}$。因此，如果圓心角為 θ，則扇形的面積 =$\mathrm{(\frac{θ}{360°})\times πr^2}$，其中 θ 是圓心角（以度為單位），r 是圓的半徑。我們還使用扇形面積公式解答了一些例題。

常見問題

1. 什麼是圓形扇形的面積？

扇形所包圍的圓形空間稱為扇形的面積。圓內由兩條半徑及其相鄰弧線所圍成的部分稱為扇形。

2. 計算圓形扇形面積的方法是什麼？

計算扇形面積的兩個主要公式是：其中 r 是圓的半徑。

$$\mathrm{圓形扇形面積 =\frac{1}{2} × r^2 θ,}$$

其中 θ 是圓心角（以弧度為單位），r 是圓的半徑。

3. 圓形扇形是什麼意思？

扇形定義為圓內由兩條半徑及其相鄰弧線所圍成的部分。半圓是圓中最常見的扇形，代表半個圓。

4. 弧線是什麼意思？

曲線的一部分或圓的一部分稱為弧線。許多物體的形狀都包含曲線。這些物體的曲線部分在數學上稱為弧線。

5. 如何根據弧長和半徑計算扇形的面積？

給定弧長和半徑，您可以計算扇形的面積。首先，使用公式弧長 $\mathrm{=(\frac{θ}{360° }) × πr^2}$ 計算弧度（θ）。現在您知道了半徑。知道了角度，您可以使用以下公式計算扇形的面積：

$$\mathrm{圓形扇形面積 =(\frac{θ}{360° }) × πr^2}$$

6. 如何根據扇形的面積求半徑？

您可以透過將值代入公式來計算半徑：

$$\mathrm{圓面積 =(\frac{θ}{360° }) × πr^2}$$

將給定值代入公式，面積 $\mathrm{= (\frac{θ}{360° }) × πr^2}$，即 $\mathrm{H.36π = (\frac{90}{360} × πr^2}$，得出 r²=144，這意味著 r = 12 個單位。

7. 如何用π表示扇形的面積？

扇形面積也可以用 π 表示。例如，如果圓的半徑為 4 個單位，扇形的圓心角為 90°，讓我們用 π 計算扇形的面積。扇形面積 = $\mathrm{=(\frac{θ}{360°}) × πr^2 }$。將值代入等式，扇形的面積 $\mathrm{= (\frac{90}{360}) × π×4^2 }$，計算結果為面積為 4π。

8. 如何用弧度計算扇形的面積？

要查詢圓心角為弧度的扇形的面積，請使用公式

$$\mathrm{面積 =\frac{1}{2} × r^2 θ, }$$

其中 θ 是圓心角（以弧度為單位），r 是圓的半徑。