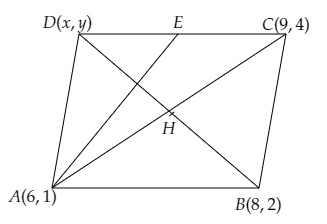
平行四邊形\( \mathrm{ABCD} \) 的三個頂點為 \( (6,1), \mathrm{B}(8,2) \) 和 \( \mathrm{C}(9,4) \)。如果 \( \mathrm{E} \) 是 \( \mathrm{DC} \) 的中點，求 \( \Delta \mathrm{ADE} \) 的面積。

已知

$A (6, 1), B (8, 2)$ 和 $C (9, 4)$ 是平行四邊形 $ABCD$ 的三個頂點。

$E$ 是 $DC$ 的中點。

要求

我們必須找到 $\triangle ADE$ 的面積。

解

設平行四邊形的第四個頂點為 (x, y)。


我們知道，平行四邊形的對角線互相平分。

連線點\( (x_{1}, y_{1}) \) 和 \( (x_{2}, y_{2}) \) 的線段的中點為\((\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}) \)

\( \mathrm{BD} \) 的中點 = \( \mathrm{AC} \) 的中點

\( \Rightarrow (\frac{8+x}{2}, \frac{2+y}{2}) \)

\( =(\frac{6+9}{2}, \frac{1+4}{2}) \)

\( \Rightarrow (\frac{8+x}{2}, \frac{2+y}{2})=(\frac{15}{2}, \frac{5}{2}) \)

比較可得，

\( \frac{8+x}{2}=\frac{15}{2} \)

\( \Rightarrow 8+x=15 \)

\( \Rightarrow x=15-8=7 \)

\( \frac{2+y}{2}=\frac{5}{2} \)

\( \Rightarrow 2+y=5 \)

\( \Rightarrow y=5-2=3 \)

平行四邊形的第四個頂點是 \( \mathrm{D}(7,3) \)。

邊 \( \mathrm{DC} \) 的中點為\((\frac{7+9}{2}, \frac{3+4}{2}) \)

\( E=(8, \frac{7}{2}) \)

頂點為$(x_{1}, y_{1}),(x_{2}, y_{2})$ 和 $(x_{3}, y_{3})$ 的 \( \Delta \mathrm{ABC} \) 的面積為$\frac{1}{2}[x_{1}(y_2-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$。

這意味著，

頂點為 \( \mathrm{A}(6,1), \mathrm{D}(7,3) \) 和 \( \mathrm{E} (8, \frac{7}{2}) \) 的 \( \Delta \mathrm{ADE} \) 的面積

\( =\frac{1}{2}[6(3-{7}{2})+7(\frac{7}{2}-1)+8(1-3)] \)

\( =\frac{1}{2}[6 \times(\frac{-1}{2})+7(\frac{5}{2})+8(-2)] \)

\( =\frac{1}{2}(-3+\frac{35}{2}-16) \)

\( =\frac{1}{2}(\frac{35}{2}-19) \)

\( =\frac{1}{2}(\frac{-3}{2}) \)

\( =\frac{-3}{4} \)

面積不能為負。

因此，\( \Delta \mathrm{ADE} \) 的面積為 \( \frac{3}{4} \) 平方單位。 

更新於： 2022 年 10 月 10 日

59 次瀏覽

開啟您的 職業生涯

透過完成課程獲得認證

開始學習
廣告