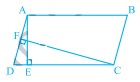
在下圖中，\( \mathrm{ABCD} \) 是一個平行四邊形，\( \mathrm{AE} \perp \mathrm{DC} \) 和 \( \mathrm{CF} \perp \mathrm{AD} \)。如果 \( \mathrm{AB}=16 \mathrm{~cm} \)、\( \mathrm{AE}=8 \mathrm{~cm} \) 和 \( \mathrm{CF}=10 \mathrm{~cm} \)，求 \( \mathrm{AD} \)。
"\n

已知

$ABCD$ 是一個平行四邊形，$AE \perp DC$ 和 $CF \perp AD$。

$AB = 16\ cm, AE = 8\ cm$ 和 $CF = 10\ cm$。

要求

我們需要求 $AD$。

解答

我們知道，

平行四邊形的面積 $=$ 底 $\times$ 高

因此，

平行四邊形 $ABCD$ 的面積 $= AB \times AE$

$= 16 \times 8$

$= 128\ cm^2$

現在，

高 $CF = 10\ cm$

這意味著，

面積 $=$ 底 $(AD)\times$ 高$(CF)$

$128 = 10 \times AD$

$AD = \frac{128}{10}$

$AD = 12.8\ cm$

因此，$AD = 12.8\ cm$。 

教程點

更新於: 2022-10-10

51 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習