資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律戴維南定理和戴維南等效電路
戴維南定理用於確定任何一個電路元件上的電流或電壓，而無需透過求解複雜的網路方程組。
戴維南定理的陳述
任何一個雙端雙向線性直流電路都可以用一個等效電路來代替，該等效電路由一個電壓源串聯一個電阻組成，電壓源等於開路負載端子上的開路電壓，電阻等於從開路負載端子看進去的電源網路的內阻。
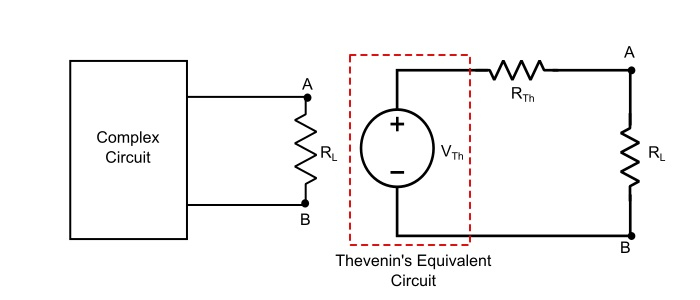
戴維南定理的解釋
步驟 1 – 去除負載電阻 (RL) 並找到開路負載端子上的開路電壓 (VOC = VTh)。
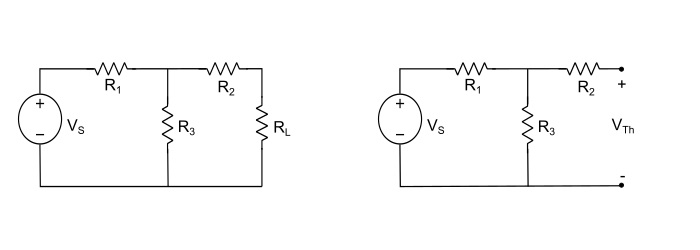
$$\mathrm{\mathit{V}_{rh}=\mathit{IR}_{3}=\mathit{V}_{s}\frac{\mathit{R}_{3}}{\mathit{R}_{1}+\mathit{R}_{3}}}$$
其中，I 是流過電阻 R1 和 R3 的閉環電流。
步驟 2 - 使恆定電源失效（對於電壓源，透過其內阻去除，對於電流源，用開路代替電源）並找到從開路負載端子看進去的內阻 (RTh)。
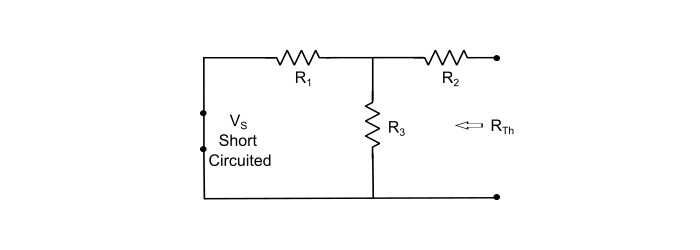
$$\mathrm{\mathit{R}_{Th}=\frac{\mathit{R}_{1}\mathit{R}_{3}}{\mathit{R}_{1}+\mathit{R}_{3}}+\mathit{R}_{2}}$$
步驟 3 獲得戴維南等效電路，將 RTh 與 VTh 串聯。將負載電阻 (RL) 重新連線到負載端子上。然後，求出負載電流。
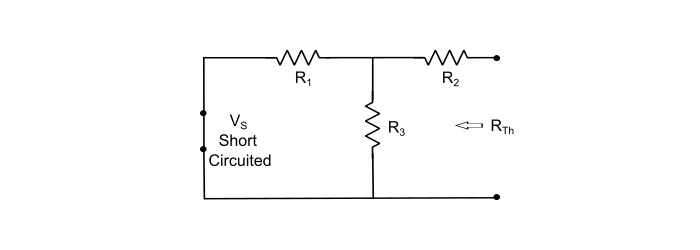
這裡，負載電流 (IL) 透過 RL 給出為：
$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}_{rh}}{\mathit{R}_{Th}+\mathit{R}_{L}}}$$
求戴維南等效電阻 (RTh) 的方法
對於獨立電源 – 包含獨立電流源或電壓源的任何線性雙向網路的 RTh 可以透過使用其內阻使電源失效來確定，即對於獨立理想電壓源，透過短路使其失效，對於獨立理想電流源，透過去除電源使其失效。然後，找到從開路負載端子看進去的網路內阻。
對於包含從屬電源或獨立電源或兩者兼而有之的電路
第一種方法 求出開路負載端子上的 VTh。接下來，短路負載端子並確定透過短路端子的短路電流 (ISC)。內阻或戴維南等效電阻由下式給出：
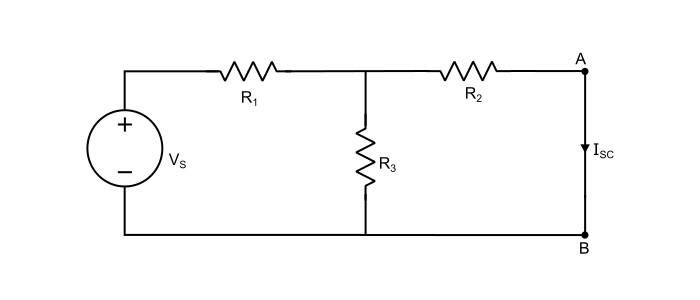
$$\mathrm{\mathit{R}_{Th}=\frac{\mathit{V}_{rh}}{\mathit{I}_{sc}}}$$
第二種方法 - 去除負載電阻並在開路負載端子上施加一個直流測試電壓 (VT)。在此期間，保持其他獨立電源失效。由於施加了 VT，直流電流 (IT) 將從負載端子流入電路。源網路的內阻或戴維南等效電阻獲得為：
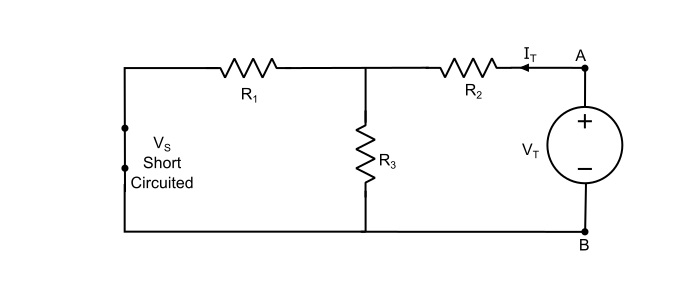
$$\mathrm{\mathit{R}_{Th}=\frac{\mathit{V}_{T}}{\mathit{I}_{T}}}$$
數值例子
使用戴維南定理，求下圖中 10 Ω 電阻中的電流。已知電池內阻為 2 Ω。
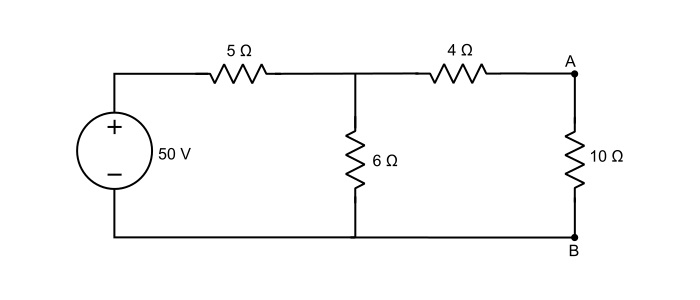
解決方案
步驟 1 – 去除負載電阻並確定負載端子上的開路電壓 (VTh)。
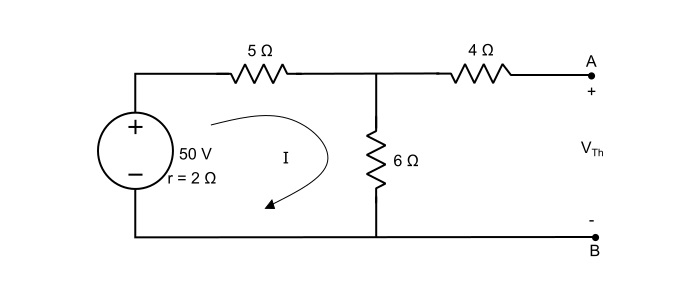
這裡，當 10 Ω 電阻被移除時，在 4 Ω 上沒有電壓降，VTh 將是出現在 6 Ω 電阻上的電壓。因此，
$$\mathrm{\mathit{I}=\frac{50}{2+5+6}=\frac{50}{13}=3.846\:A}$$
當 10 Ω 電阻被移除時，在 4 Ω 電阻上沒有電壓降，VTh 將是出現在 6 Ω 電阻上的電壓。因此，
$$\mathrm{\mathit{V}_{Th}=\mathit{I}×6=3.846×6=23.076\:V}$$
步驟 2 – 要找到 RTh，請使所有獨立電源失效。如，
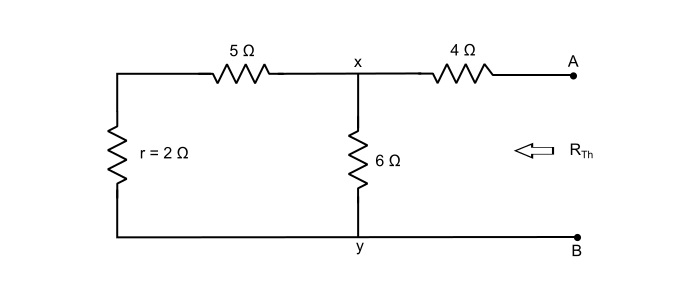
$$\mathrm{\mathit{R}_{xy}=(5+2)||6=\frac{7×6}{7+6}=3.23\:Ω}$$
$$\mathrm{\mathit{R}_{Th}=\mathit{R}_{xy}+4=3.23+4=7.23 \:Ω}$$
步驟 3 – 構造戴維南等效電路並將負載電阻重新連線以計算負載電流，如，
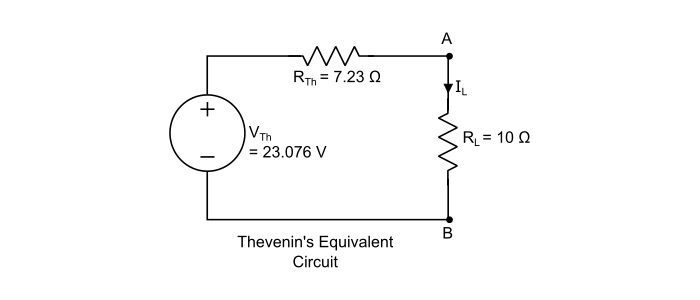
$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}_{rh}}{\mathit{R}_{rh}+\mathit{R}_{L}}=\frac{23.076}{7.23+10}=1.339\:A}$$
2K+ 瀏覽量
