資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會科學
時尚研究
法律研究磁路——串聯和並聯磁路
磁路
磁路定義為磁通量跟隨的閉合路徑。
磁路由高導磁率材料製成的芯組成，如鐵和軟鋼等。這是因為這些材料對磁通量的流動阻力很小。
考慮在鐵芯上繞有 N 圈的線圈（見圖）。當電流 I 流過線圈時，便會形成磁通量 (ψ)。此磁通量遵循閉合路徑 ABCDA，因此 ABCDA 為磁路。
在磁路中，磁芯中的磁通量大小取決於電流 (I)和匝數 (N)。NI 的乘積被稱為磁動勢 (MMF)。
$$\mathrm{MMF = NI= 安培-匝數}$$
磁路對磁通量流動產生的阻力稱為磁路的磁阻 (S)。磁路的磁阻取決於磁路的長度、磁路的橫截面積和組成磁路的材料的特性。
磁路型別
磁路有兩種型別：
- 串聯磁路
- 並聯磁路
串聯磁路
當相同磁通量 ψ 流過磁路的每個部分時，則該磁路被稱為串聯磁路。
考慮一個由不同相對磁導率的不同磁性材料組成的複合串聯磁路（具有不同尺寸和材料的部分的串聯磁路稱為複合串聯磁路）。該串聯磁路的每個部分都將對磁通量 ψ 產生磁阻。由於磁路的不同部分串聯，因此總磁阻等於各個部分的磁阻之和。
引用串聯磁路的圖形，我們有，
$$\mathrm{總磁阻，S_T=\frac{l_1}{\mu_0\mu_r1a_1}+\frac{l_2}{\mu_0\mu_r2a_2}}$$
$$\mathrm{總 MMF = 磁通量 \times 總磁阻}$$
$$\mathrm{\Longrightarrow 總 MMF =\mathit{ψ(\frac{l_1}{\mu_0\mu_r1a_1}+\frac{l_2}{\mu_0\mu_r2a_2}}})}$$
$$\mathrm{\Longrightarrow 總 MMF =\mathit{(\frac{B_1}{\mu_0\mu_r2}})\times l_1+(\frac{B_2}{\mu_0\mu_r2}})\times l_2}}}$$
$$\mathrm{\Longrightarrow 總 MMF = \mathit{H_1\times l_1+H_2\times l_2}}}$$
因此，在串聯磁路中建立磁通量所需的總 MMF 是該電路各部分所需 MMF 的總和。
並聯磁路
一個有多條磁通量路徑的磁路稱為並聯磁路。
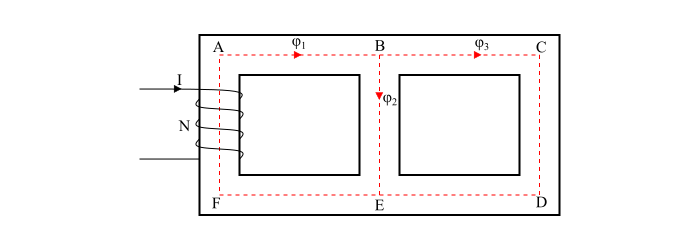
考慮線圈 N 匝繞線上路 AF 上，載有 I 安培的電流。線圈建立的磁通量 $\varphi_1$ 在 B 處分成兩條路徑 -
- 磁性 $\varphi_2$ 沿著路徑 BE 傳遞。
- 磁通量 $\varphi_3$ 沿著路徑 BCDE 傳遞。
因此，總通量為，
$$\mathrm{\mathit{\varphi_1=\varphi_2+\varphi_3}}}$$
路徑 BE 和 BCDE 互為並聯，從而形成並聯磁路。在並聯磁路中，整個並聯磁路所需的 MMF 等於任何一條並聯路徑所需的 MMF。
假設
$$\mathrm{\mathit{S_1} = 磁路 ABEF 的磁阻}$$
$$\mathrm{\mathit{S_2} = 磁路 BE 的磁阻}$$
$$\mathrm{\mathit{S_3} = 磁路 BCDE 的磁阻}$$
因此，
$$\mathrm{總 MMF = 路徑 ABEF 的 MMF + 路徑 BE 或 BCDE 的 MMF}$$
$$\mathrm{\Longrightarrow 總 MMF = \mathit{\varphi_1S_1+ ψ_2S_2+ \varphi_3S_3}}}$$
16K+ 瀏覽量
