如何計算等效電阻（串聯和並聯電路示例）

---

在電氣和電子電路中，電阻被定義為導體材料對電流（或電荷）流動產生的摩擦量。用於在電路中引入電阻的電路元件稱為電阻器。電阻器是一種無源電路元件，它控制著電流透過電路的流動，並將多餘的電能轉化為熱能。有時，我們需要的電路中所需的電阻值沒有現成的電阻器。因此，我們會以特定的方式將兩個或多個電阻器連線起來，以獲得電路中所需的電阻值。

在本教程中，我們將瞭解等效電阻是什麼，以及當電阻器串聯或並聯或串並聯連線時，如何確定它們的等效電阻。我們還將討論三種組合的數值示例，以便更好地理解這個概念。

如何在串聯電路中計算等效電阻？

一種電阻器組合方式，其中電阻器首尾相連，形成鏈狀，並且只提供一條電流路徑，稱為電阻器的串聯連線，或簡稱為串聯電阻。

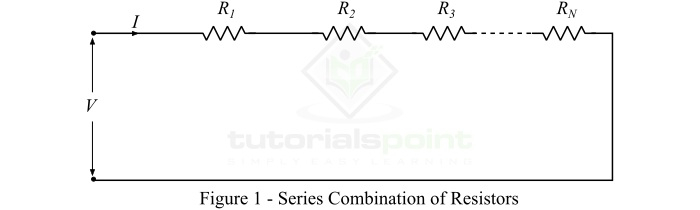
為了理解串聯等效電阻的計算，考慮N個電阻，分別為R₁、R₂、R₃……R_N，串聯連線，如圖1所示。假設組合的總電壓為V伏特，I為組合的總電流。需要注意的是，電流I對所有電阻器都是相同的。

根據歐姆定律，我們有：

$$\mathrm{V_{1}=IR_{1};\: V_{2}=IR_{2};\: \cdot \cdot \cdot V_{N}=IR_{N}}$$

此外，

$$\mathrm{V=V_{1}+V_{2}+V_{3}+\cdot \cdot \cdot + V_{N}}$$

$$\mathrm{\Rightarrow V=IR_{1}+IR_{2}+IR_{3}+\cdot \cdot \cdot + IR_{N}}$$

$$\mathrm{\Rightarrow V=I\left ( R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot + R_{N} \right )}$$

但是，

$$\mathrm{\frac{V}{I}=R_{eq}}$$

因此，

$$\mathrm{R_{eq}=R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot +R_{N}}$$

因此，當多個電阻器串聯連線時，串聯組合的等效電阻可以透過簡單地將所有電阻值相加來計算。

特殊情況 - 當N個相同電阻值（例如R）的電阻器串聯連線時，它們的等效電阻由以下公式計算：

$$\mathrm{R_{eq}=N\times R}$$

其中，N是串聯組合的電阻器總數。

以下是關於電阻器串聯組合的一些重要要點，您應該注意：

• 串聯組合的等效電阻等於所有電阻之和。

• 串聯電阻組合的等效電阻始終大於組合中最大的電阻。

• 透過串聯所有電阻的電流相同。

• 每個電阻上的壓降不同，取決於電阻值。

• 電阻器串聯連線是為了將電壓分成多個較小的電壓值。

如何在並聯電路中計算等效電阻？

一種電阻器組合方式，其中所有電阻器的一端連線到一個公共點，另一端連線到另一個公共點，使得電阻器數量和電流路徑數量相等，稱為電阻器的並聯組合。

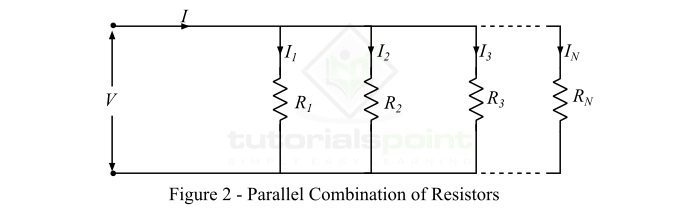
現在，為了理解並聯電阻組合的等效電阻計算過程，考慮N個電阻並聯連線，如圖2所示。從圖2可以看出，所有電阻器上的電壓相同，都等於V伏特，但每個電阻器上的電流不同，取決於電阻值。

根據歐姆定律，

$$\mathrm{I_{1}=\frac{V}{R_{1}};\:I_{2}=\frac{V}{R_{2}};\: I_{3}=\frac{V}{R_{3}};\: \cdot \cdot \cdot I_{N}=\frac{V}{R_{N}} }$$

此外，

$$\mathrm{I=I_{1}+I_{2}+I_{3}+ \cdot \cdot \cdot +I_{N}}$$

$$\mathrm{\Rightarrow I=\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}}+ \cdot \cdot \cdot +\frac{V}{R_{N}}}$$

$$\mathrm{\Rightarrow I=V\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+ \cdot \cdot \cdot +\frac{1}{R_{N}} \right )}$$

但是，

$$\mathrm{\frac{I}{V}=\frac{1}{R_{eq}}}$$

因此，

$$\mathrm{\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+ \cdot \cdot \cdot +\frac{1}{R_{N}}}$$

因此，當多個電阻並聯連線時，組合的等效電阻的倒數等於各個電阻倒數之和。

當只有兩個電阻並聯連線時，等效電阻由以下公式給出：

$$\mathrm{\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}=\frac{R_{1}+R_{2}}{R_{1}R_{2}}}$$

$$\mathrm{\therefore R_{eq}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}}$$

因此，當兩個電阻並聯連線時，組合的等效電阻等於兩個電阻的乘積除以它們的和。

特殊情況 - 當所有N個並聯連線的電阻器具有相同的電阻值（例如R）時，組合的等效電阻由以下公式給出：

$$\mathrm{ R_{eq}=\frac{R}{N}}$$

以下是關於電阻器並聯組合的一些重要要點：

• 並聯電阻組合的等效電阻小於組合中最小的電阻。

• 透過每個電阻的電流不同。

• 所有電阻器上的電壓相同。

• 並聯電阻組合充當分流器，因為它將單個電流分成多個電流。

串並聯電阻組合的等效電阻

有時，我們會遇到一些電路，其中一些電阻器串聯連線，另一些電阻器並聯連線。這種電阻器組合通常被稱為串並聯電阻組合。圖3顯示了一個電阻網路，其中電阻器以串並聯方式連線。

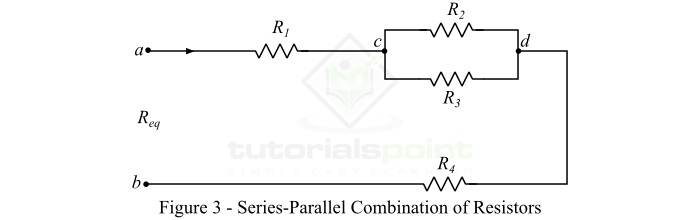
串並聯電阻組合的等效電阻可以透過以下兩個步驟計算：

步驟1

計算所有並聯連線電阻器的等效電阻。對於給定的示例，我們有：

$$\mathrm{ R_{cd}=\frac{R_{2}R_{3}}{R_{2}+R_{3}}}$$

步驟2

計算串聯連線電阻器的等效電阻。因此，對於給定的示例，我們有：

$$\mathrm{ R_{eq}=R_{1}+R_{cd}+R_{4}}$$

或者

$$\mathrm{ R_{eq}=R_{1}+\left ( \frac{R_{2}R_{3}}{R_{2}+R_{3}} \right )+R_{4}}$$

數值示例（1）

計算以下電阻網路的等效電阻：

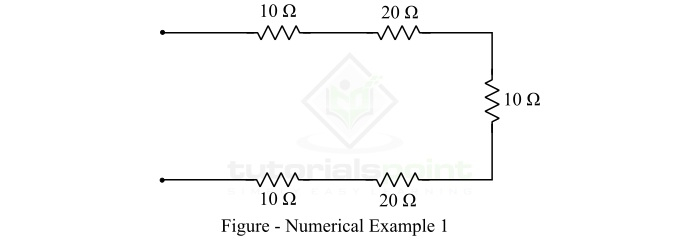
解決方案

可以觀察到，在給定的網路中，電阻器是串聯組合的。因此，它們的等效電阻將為：

$$\mathrm{ R_{eq}=10 + 20 + 10 + 20 + 10}$$

$$\mathrm{ R_{eq}=70\: \Omega }$$

數值示例（2）

計算以下電阻網路的等效電阻：

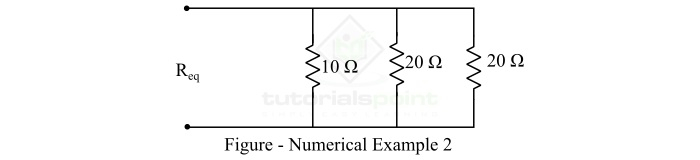
解決方案

透過觀察，可以清楚地看出網路中的電阻器是並聯排列的。因此，組合的等效電阻將為：

$$\mathrm{\frac{1}{R_{eq}} =\frac{1}{10}+\frac{1}{20}+\frac{1}{20} }$$

$$\mathrm{\frac{1}{R_{eq}} =\frac{2 + 1 + 1}{20}+=\frac{4}{20}}$$

$$\mathrm{\therefore R_{eq} =5 \: \Omega } $$

數值示例（3）

計算以下電阻網路的等效電阻。

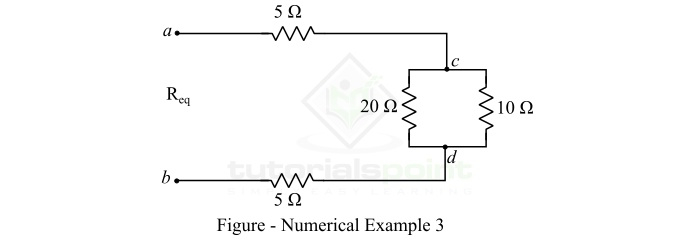
解決方案

我們可以看到，該網路有一些電阻器串聯連線，也有一些電阻器並聯連線。

10歐姆和20歐姆並聯電阻的等效電阻為：

$$\mathrm{ R_{cd} =\frac{10\times 20}{10+20} } $$

$$\mathrm{\Rightarrow R_{cd} =\frac{ 200}{30}=6.67\, \Omega }$$

現在，所有電阻器都串聯連線。因此，網路的等效電阻為：

$$\mathrm{ R_{eq} =5 + 6.67 + 5=16.67\, \Omega } $$

結論

在本教程中，我們討論了電阻器集合可以以三種方式組合：串聯、並聯和串並聯。在串聯組合中，組合的等效電阻等於所有電阻之和。在並聯組合中，組合的等效電阻的倒數等於各個電阻倒數之和。

根據電路的要求或為了在電路中引入所需的電阻值，當沒有特定電阻值的單個電阻器可用時，電阻器會以串聯或並聯的方式組合。