對於下列電阻組合電路，求A-B之間的等效電阻R_EQ。

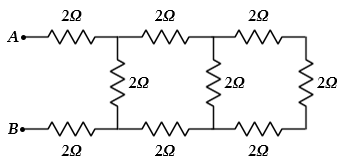
為了找到下列梯形網路電阻（它只是串聯和並聯電阻的組合）組合電路的等效電阻R_EQ，我們將從右側開始。

我們知道計算串聯電路的公式如下：

R_t = R₁ + R₂ + R₃ + R₄ +...... 其中R_t是總電阻，R₁, R₂, R₃, 和 R₄是串聯連線的各個電阻的阻值。

使用串聯電路的簡化公式，對於三個串聯電阻，我們可以找到R₇、R₈和R₉組合的等效電阻，並將其稱為R_A。

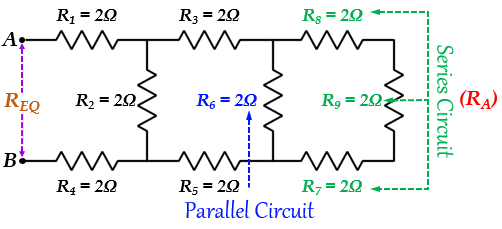
因此，總電阻可以計算為R_A，如上所示-

R_A = R₇ + R₈ + R₉

R_A = 2 + 2 + 2

R_A = 6Ω

此值為R_A = 6Ω的電阻值現在與R₆並聯。

我們知道計算並聯電路的公式如下：

R_t = 1 / R₁ + 1 / R₂ + 1 / R₃ + 1 / R₄.... 其中R_t是總電阻，R₁, R₂, R₃, 和 R₄是串聯連線的各個電阻的阻值。

使用此並聯電路公式，對於兩個並聯電阻，我們可以找到R_A和R₆組合的總電阻，並將其稱為R_B。

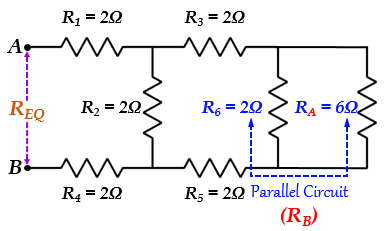
因此，總電阻可以計算為R_B，如上所示-

$\frac{1}{{R}_{B}}=\frac{1}{{R}_{A}}+\frac{1}{{R}_{6}}$

$\frac{1}{{R}_{B}}=\frac{1}{6}+\frac{1}{2}\Leftrightarrow \frac{2+6}{6\times 2}\Leftrightarrow \frac{8}{12}\Rightarrow \frac{2}{3}$

${R}_{B}=\frac{3}{2}$

R_B = 1.5Ω

此值為R_B = 1.5Ω的電阻值現在與R₃ & R₅串聯。

使用串聯電路的簡化公式，對於三個串聯電阻，我們可以找到R_B、R₃和R₅組合的等效電阻，並將其稱為R_C。

因此，總電阻可以計算為R_C，如上所示-

R_C = R_B + R₃ + R₅

R_C = 1.5 + 2 + 2

R_C = 5.5Ω

此值為R_C = 5.5Ω的電阻值現在與R₂並聯。

使用並聯電路公式，對於兩個並聯電阻，我們可以找到R_C和R₂組合的總電阻，並將其稱為R_D。

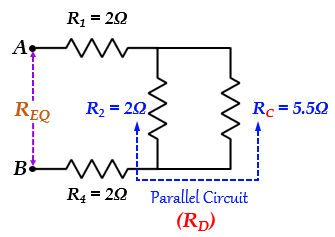
因此，總電阻可以計算為R_D，如上所示-

$\frac{1}{{R}_{D}}=\frac{1}{{R}_{C}}+\frac{1}{{R}_{2}}$

$\frac{1}{{R}_{D}}=\frac{1}{5.5}+\frac{1}{2}\Leftrightarrow \frac{2+5.5}{5.5\times 2}\Leftrightarrow \frac{7.5}{11}\Rightarrow \frac{75}{110}$

${R}_{D}=\frac{110}{75}$

R_D = 1.46Ω

此值為R_D = 1.46Ω的電阻值現在與R₁ & R₄串聯。

使用串聯電路的簡化公式，對於三個串聯電阻，我們可以找到R_D、R₁和R₄組合的總電阻，並將其稱為R_t。

因此，總電阻可以計算為R_t，如上所示-

R_t = R_D + R₁ + R₄

R_t = 1.46 + 2 + 2

R_t = 5.46Ω

因此，上述複雜的組合電阻網路包含九個單獨的電阻，它們以串聯和並聯組合連線在一起，可以用一個值為5.46Ω的單一等效電阻(R_EQ)代替。

Tutorialspoint

更新於：2022年10月10日

211 次瀏覽

開啟你的職業生涯

完成課程後獲得認證

開始學習