資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究感應電動機的等效電路、定子電路模型和轉子電路模型
感應電動機的執行原理是基於定子電路在轉子電路中感應電壓和電流。感應電動機穩態條件下的效能特性可以透過其等效電路進行評估。由於三相感應電動機表示一個平衡負載，因此，其等效電路僅繪製一相。
感應電動機的定子電路模型
感應電動機的定子電路模型或定子等效電路如圖所示。
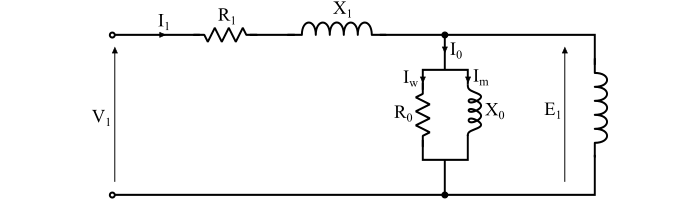
感應電動機的定子電路模型包括定子相繞組電阻R1、定子相繞組漏抗X1。R1和X1直接出現在電機模型的輸入端。純感性電抗X0表示感應電動機的勵磁電抗，其值遠大於其他電抗。非感性電阻R0表示感應電動機的鐵損分量。因此，感應電動機的空載電流I0由勵磁電抗（X0）所產生的勵磁電流（Im）和鐵損電阻（R0）所產生的鐵損電流Iw的相量和給出。因此，
$$\mathrm{𝐼_0 = 𝐼_𝑚 + 𝐼_𝑤 … (1)}$$
由於感應電動機的空氣隙導致較高的磁阻，因此感應電動機的空載電流（I0）非常大（約為額定電流的25%到40%）。
感應電動機的轉子電路模型
當三相電源電壓施加到感應電動機的定子繞組時，會在感應電動機的轉子繞組中感應出電壓。實際上，轉子和定子旋轉磁場之間的相對運動越大，感應的轉子電壓就越大。
當轉子靜止時，相對運動最大。這種情況稱為靜止狀態或鎖轉狀態或堵轉狀態。
如果靜止狀態下的感應轉子電壓為E20，則任何滑差值下的感應轉子電壓由下式給出：
$$\mathrm{𝐸_2 = 𝑠𝐸_{20} … (2)}$$
轉子電路的電阻（R2）是恆定的，並且與感應電動機的滑差無關。
感應電動機的轉子電路的電抗取決於轉子繞組的電感和轉子電流的頻率。因此，如果L2是轉子的電感，則滑差s下的轉子電抗由下式給出：
$$\mathrm{𝑋_2 = 2𝜋𝑓_2𝐿_2}$$
但轉子頻率為：
$$\mathrm{𝑓_2 = 𝑠𝑓_1}$$
$$\mathrm{\therefore\: 𝑋_2 = 2𝜋𝑠𝑓_1𝐿_2 = 𝑠(2𝜋𝑓_1𝐿_2) = 𝑠𝑋_{20} … (3)}$$
其中，X20是靜止轉子電抗。
滑差s下轉子的阻抗由下式給出：
$$\mathrm{𝑍_2 = 𝑅_2 + 𝑗𝑋_2 = 𝑅_2 + 𝑗𝑠𝑋_{20} … (4)}$$
因此，感應電動機的每相轉子電流由下式給出：
$$\mathrm{𝐼_2 =\frac{𝐸_2}{𝑍_2}=\frac{𝑠𝐸_{20}}{𝑅_2 + 𝑗𝑠𝑋_{20}}… (5)}$$
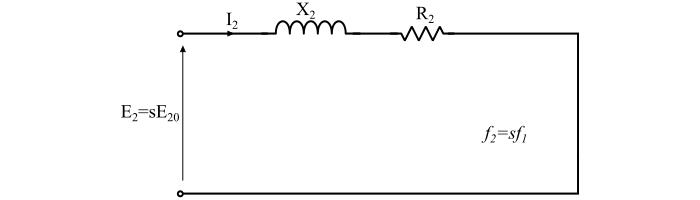
使用此轉子電流方程，可以繪製出感應電動機的轉子電路模型，如圖所示。
885 次瀏覽
