雙籠式感應電動機的等效電路

對於雙籠式感應電動機，下標“s”和“r”分別表示定子和轉子。

設：

• 𝑅_𝑠 = 每相定子電阻
• 𝑋_𝑠 = 每相定子電抗
• 𝑅′_𝑟𝑜 = 外籠每相轉子電阻（折算到定子）
• 𝑋′_𝑟𝑜 = 外籠每相靜止漏電抗（折算到定子）
• 𝑅′_𝑟𝑖 = 內籠每相轉子電阻（折算到定子）
• 𝑋′_𝑟𝑖 = 內籠每相靜止漏電抗（折算到定子）
• 𝑠 = 滑差率

如果認為主磁通完全穿過兩個籠子，則可以認為兩個籠子的阻抗是並聯的。圖1顯示了滑差為s的雙籠式感應電動機的等效電路。

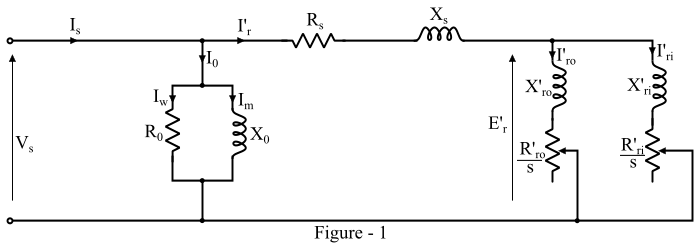
此處，轉子阻抗由下式給出：

$$\mathrm{外籠阻抗,\: 𝑍′_{𝑟𝑜} =\frac{𝑅′_{𝑟0}}{𝑠}+ 𝑗𝑋′_{𝑟𝑜}}$$

$$\mathrm{內籠阻抗,\: 𝑍\:′_{𝑟𝑖} =\frac{𝑅′_{𝑟𝑖}}{𝑠}+ 𝑗𝑋′_{𝑟𝑖}}$$

並且，定子阻抗由下式給出：

$$\mathrm{定子阻抗, \:𝑍_𝑠 = 𝑅_𝑠 + 𝑗𝑋_𝑠}$$

在等效電路中，如果忽略包含R0和X0的並聯支路，則可以得到雙籠式感應電動機的近似等效電路，如下圖所示。

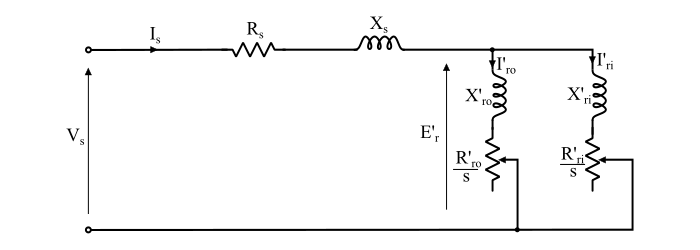
折算到定子的電動機每相等效阻抗由下式給出：

$$\mathrm{𝑍_{𝑒𝑠} = 𝑍_𝑠 + (𝑍′_{𝑟𝑜} || 𝑍′_{𝑟𝑖})}$$

$$\mathrm{⇒ 𝑍_{𝑒𝑠} = (𝑅_𝑠 + 𝑗𝑋_𝑠) + (\frac{𝑍′_{𝑟𝑜} 𝑍′_{𝑟𝑖}}{𝑍′_{𝑟𝑜}+ 𝑍′_{𝑟𝑖}})}$$

流過轉子外籠的電流由下式給出：

$$\mathrm{𝐼′_{𝑟𝑜} =\frac{𝐸′_𝑟}{𝑍′_{𝑟𝑜}}}$$

流過轉子內籠的電流由下式給出：

$$\mathrm{𝐼′_{𝑟𝑖} =\frac{𝐸′_𝑟}{𝑍′_{𝑟𝑖}}}$$

因此，折算到定子的轉子電流等於外籠和內籠電流的相量和，即：

$$\mathrm{𝐼′_𝑟 = 𝐼′_{𝑟𝑜} + 𝐼′_{𝑟𝑖}}$$

Manish Kumar Saini

更新於：2021年8月25日

瀏覽量：1000+

開啟你的職業生涯

完成課程獲得認證

開始學習