資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究雙籠式感應電動機的轉矩-滑差特性及籠型轉矩比較
雙籠式感應電動機的轉矩-滑差特性
在雙籠式感應電動機中，假設兩個籠型產生兩個獨立的轉矩。因此，雙籠式感應電動機產生的總轉矩等於兩個籠型轉矩之和。圖中顯示了兩個籠型的轉矩-滑差特性和電動機的總轉矩。
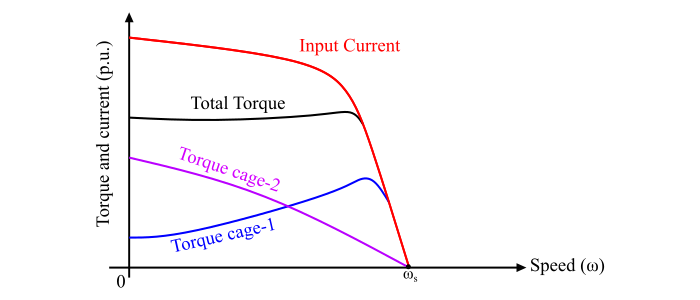
透過改變各個籠型的電阻和漏抗，可以根據需要修改所得的轉矩-速度特性。可以透過改變轉子條的橫截面積來改變電阻，而可以透過改變槽口的寬度和內籠的深度來改變漏抗。
雙籠式感應電動機籠型轉矩比較
參考圖 1 所示的雙籠式感應電動機的等效電路 -
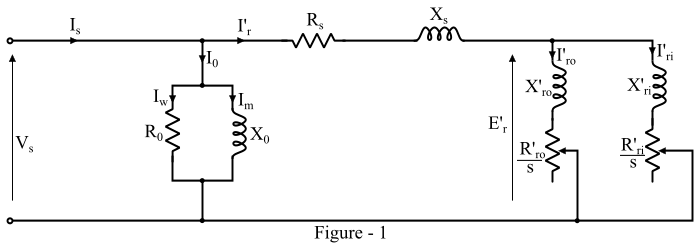
內轉子籠每相產生的功率由下式給出：
$$\mathrm{𝑃_{𝑑𝑖} =\frac{𝐼′_{𝑟𝑖}^{2}𝑅'_{𝑟𝑖}}{𝑠}… (1)}$$
外轉子籠每相產生的功率為：
$$\mathrm{𝑃_{𝑑𝑜} =\frac{𝐼′_{𝑟𝑜}^2𝑅'_{𝑟𝑜}}{𝑠}… (2)}$$
因此，兩個籠型每相產生的總功率為：
$$\mathrm{𝑃_𝑑 = 𝑃_{𝑑𝑖} + 𝑃_{𝑑𝑜} =\frac{𝐼′_{𝑟𝑖}^{2}𝑅'_{𝑟𝑖}}{𝑠}+\frac{𝐼′_{𝑟𝑜}^2𝑅'_{𝑟𝑜}}{𝑠}… (3)}$$
此外，
$$\mathrm{𝐼′_{𝑟𝑜} =\frac{𝐸′_𝑟}{𝑍′_{𝑟𝑜}}… (4)}$$
$$\mathrm{𝐼′_𝑟𝑖 =\frac{𝐸′_𝑟}{𝑍′_{𝑟𝑖}}… (5)}$$
$$\mathrm{𝑍′_{𝑟𝑜} = \sqrt{(\frac{𝑅′_{𝑟𝑜}}{𝑠})^2+ (𝑋′_{𝑟𝑜})^2} … (6)}$$
以及，
$$\mathrm{𝑍′_{𝑟𝑖} = \sqrt{(\frac{𝑅′_{𝑟i}}{𝑠})^2+ (𝑋′_{𝑟i})^2} … (7)}$$
現在，設：
- τ𝑑𝑖 = 內籠產生的轉矩
- τ𝑑𝑜 = 外籠產生的轉矩
- τ𝑑 = 兩個籠型產生的總轉矩
因此，產生的總功率以及由此產生的總轉矩由下式給出：
$$\mathrm{𝑃_𝑑 = 2𝜋𝑛_𝑠\tau_𝑑}$$
$$\mathrm{\therefore \tau_𝑑 =\frac{𝑃_𝑑}{2𝜋𝑛_𝑠}}$$
$$\mathrm{⇒ 𝜏𝑑 =\frac{1}{2𝜋𝑛_𝑠}(\frac{𝐼′_{𝑟𝑖}^2𝑅'_{𝑟𝑖}}{𝑠}+\frac{𝐼′_{𝑟𝑜}^2𝑅'_{𝑟𝑜}}{𝑠}) … (8)}$$
因此，外籠轉矩與內籠轉矩的比率為：
$$\mathrm{\frac{\tau_{𝑑𝑜}}{\tau_{𝑑𝑖}}=\frac{(\frac{𝑅′_{𝑟𝑜}}{𝑠})^2+ (𝑋′_𝑟𝑜)^2}{(\frac{𝑅′_{𝑟o}}{𝑠})^2+ (𝑋′_{𝑟𝑖})^2}… (9)}$$
2K+ 次瀏覽
