直立圓柱體

---

引言

一個三維立體圖形稱為直立圓柱體。直立圓柱體的兩端都有一個封閉的圓形表面，並且互相平行。直立圓柱體也稱為直圓柱體。封閉表面上的所有點都與直立圓柱體的軸線等距。在日常生活中，直立圓柱體是最常見的3D圖形。透過堆疊許多圓形的紙片可以建立一個直立圓柱體。因為它與圓形底面成直角，所以被稱為直立圓柱體。本教程將涵蓋直立圓柱體的表面積、體積和特性。

直立圓柱體

直立圓柱體是由兩個平行的底面和一個封閉的曲面構成的三維立體形狀，每個底面都類似於圓盤狀的圓形。直圓柱體的軸線是連線兩個圓形底面中心或穿過其中心的直線。高度，或“ℎ”，代表垂直距離，即圓柱體兩個底面之間的距離。直立圓柱體的半徑，用“𝑟”表示，是從中心到任一兩個底面外邊界。因此，兩個圓和一個矩形組合起來構成一個直立圓柱體。請看直立圓柱體構造圖。

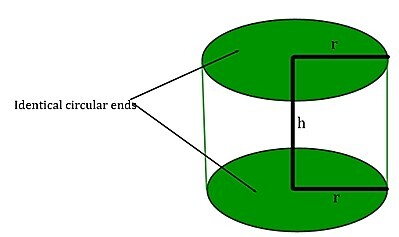
圓柱體的表面積

直立圓柱體的表面所覆蓋的面積稱為直立圓柱體的表面積。直立圓柱體的表面區域可以分為兩類：

直立圓柱體的曲面面積

它也被稱為直立圓柱體的側面積。它是直立圓柱體平行圓形底面之間的空間，由圓柱體的曲面覆蓋。因此，求直立圓柱體側面積的公式為：

$$\mathrm{C.S.A\:=\:2\pi\:rh}$$

直立圓柱體的總表面積

它被描述為圓柱體充滿的區域。這個區域包含兩個圓和一個曲面。因此，為了計算直立圓柱體的總表面積，我們將兩個圓的面積和曲面的面積加起來。

$$\mathrm{T.S.A\:=\:2\pi\:rh\:+\:2\pi\:r^{2}\:=\:2\pi\:r(r\:+\:h)}$$

例題

求半徑為1毫米，高為7毫米的圓柱體的側面積和總表面積。

解：

已知 𝑟 = 1毫米，ℎ = 7毫米

$\mathrm{C.S.A\:=\:2\pi\:rh\:=\:2\:\times\:\frac{22}{7}\:\times\:1\:\times\:7\:=\:44mm^{2}}$

$\mathrm{T.S.A\:=\:2\pi\:r(r\:+\:h)\:=\:2\:\times\:\frac{22}{7}\:\times\:1\:\times\:(1\:+\:7)\:=\:\frac{44\:\times\:8}{7}\:=\:50.285\:mm^{2}}$

圓柱體的體積

直立圓柱體在空間中佔據的面積稱為體積。直立圓柱體的體積用立方單位表示，如$\mathrm{(m^{3},\:cm^{3},\:in^{3}\:or\:ft^{3})}.$

對於任何高為“ℎ”和半徑為“𝑟”的直立圓柱體，其體積公式如下：體積 = 高度 × 圓的面積。因此，求直立圓柱體體積的公式為：

$$\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$$

例題

半徑為5釐米，高為35釐米的圓柱形水箱的容量是多少？

解：

求直立圓柱體體積的公式為：

$$\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$$

已知 $\mathrm{r\:=\:5cm\:,\:h\:=\:35cm}$

因此：

$\mathrm{V\:=\:\pi\:r^{2}h\:=\:\frac{22}{7}\:\times\:5\:\times\:5\:\times\:35\:=\:22\:\times\:125\:=\:2750cm^{3}}$

因此，圓柱形水箱的容量是2750 𝑐𝑚³

解題示例

1. 半徑為2米，曲面面積為110平方米的圓柱體的高度是多少？

求直立圓柱體側面積的公式為

$$\mathrm{C.S.A\:=\:2\pi\:rh}$$

$$\mathrm{110\:=\:2\:\times\:\frac{22}{7}\:\times\:2\:\times\:h}$$

$$\mathrm{h\:=\:\frac{110\:\times\:7}{4\:\times\:22}\:=\frac{35}{4}\:=\:8.75m}$$

因此，直立圓柱體的高度是8.75米

2. 直徑為8釐米，高為直徑的$\mathrm{\frac{7}{2}}$的圓柱形燒瓶的體積是多少？

解：

求直立圓柱體體積的公式為，$\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$

已知 $\mathrm{r\:=\:\frac{8}{2}\:=\:4cm\:,\:h\:=\:\frac{7}{2}\:\times\:8cm\:=\:28cm\:V\:=\:\pi\:r^{2}h\:=\:\frac{22}{7}\:\times\:4^{2}\:\times\:28\:=\:22\:\times\:4^{3}\:=\:1408\:cm^{3}}$

因此，圓柱形燒瓶的體積是1408 𝑐𝑚³

3. 半徑為7米，高為20米的圓柱形帳篷需要多大面積的篷布？

解：

圓柱形帳篷如下：

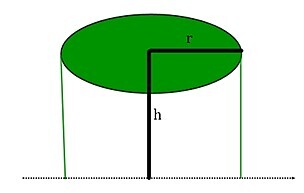
帳篷的總表面積為：

$\mathrm{T.S.A\:=\:2\pi\:rh\:+\:\pi\:r^{2}}$

已知，$\mathrm{r\:\:7m,\:h\:=\:20m}$

所需的篷布總面積為

$$\mathrm{=\:2\pi\:rh\:+\:\pi\:r^{2}\:=\:\pi\:r(2h\:+\:r)}$$

$$\mathrm{=\:\frac{22}{7}\:\times\:7(40\:+\:7)\:=\:22\:\times\:47\:=\:1034\:m^{2}}$$

因此，所需的篷布面積是1034 平方米

4. 體積為200立方厘米，高為5釐米的圓柱體的半徑是多少？使用𝜋 = 3.14。

解：

求直立圓柱體體積的公式為 $\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$

已知 $\mathrm{V\:=\:200cm^{3}\:,\:h\:=\:5cm}$

$$\mathrm{200\:=\:3.14\:\times\:r^{2}\:\times\:5}$$

$$\mathrm{r^{2}\:=\:\frac{200}{15.7}\:=\:\frac{2000}{157}\:=\:12.74}$$

$$\mathrm{r\:=\:\sqrt{12.74}\:=\:3.57cm}$$

5. 如果直立圓柱體的半徑為𝑝單位，高為𝑞單位，寫出計算其曲面面積、總表面積和體積的公式。

解：

$$\mathrm{C.S.A\:=\:2\pi\:rh\:=\:2\pi\:pq}$$

$$\mathrm{T.S.A\:=\:2\pi\:r(r\:+\:h)\:=\:2\pi\:p(p\:+\:q)}$$

$$\mathrm{V\:=\:\pi\:r^{2}h\:=\:\pi\:p^{2}q}$$

結論

• 求直立圓柱體側面積的公式為 $\mathrm{C.S.A\:=\:2\pi\:rh}$

• $\mathrm{T.S.A\:=\:2\pi\:rh\:+\:2\pi\:r^{2}\:=\:2\pi\:r(r\:+\:h)}$ 是求直立圓柱體總表面積的公式。

• 求直立圓柱體體積的公式為 $\mathrm{Volume\:=\:V\:=\:\pi\:r^{2}h}$

常見問題

1. 你如何稱呼圓柱體的邊緣？

圓錐、球體和圓柱體沒有平坦的側面，因此它們沒有邊緣。頂點是兩條或多條邊匯合的地方。

2. 直立圓柱體的底面是橢圓形嗎？

直立圓柱體有兩個平坦的底面，三個側面和一個曲面。

3. 圓柱體可以有多少個維度？

圓柱體源於希臘字母o，羅馬化後為kulindros，意思是“滾筒”或“滾筒”，歷史上一直是最基本的曲線幾何形狀之一。它是三維的。

4. 存在多少種不同型別的圓柱體？

兩種最常用的液壓缸型別是單作用和雙作用液壓缸。

5. 圓柱體上是否存在平行線？

圓柱體是一種3D立體形狀，由兩個平行且相同的底面和一個曲面連線而成。這些底面類似於圓盤。圓柱體的軸線是穿過中心或連線兩個圓形底面中心的直線。

6. 圓柱體的曲面叫什麼？

總表面積是指圓柱體所有側面的曲面，不包括底面的面積。

7. 圓柱體不是稜柱，為什麼？

稜柱不是旋轉幾何圖形，而圓柱體是。稜柱有兩個平坦的矩形面和兩個多邊形作為其兩端，而圓柱體有兩個平坦的端面和一個曲面。稜柱有多條對角線，而圓柱體沒有。