資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學離散時間訊號的表示
離散時間訊號
僅在離散時間點定義的訊號稱為離散時間訊號。離散時間訊號用x(n)表示，其中n是時域中的自變數。
離散時間訊號的表示
離散時間訊號可以用以下四種方式表示：
- 圖形表示
- 函式表示
- 表格表示
- 序列表示
離散時間訊號的圖形表示
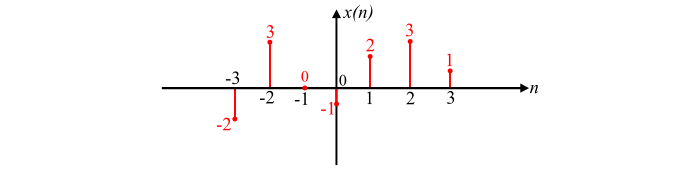
考慮一個離散時間訊號x(n)，其值為：
- x(−3) = −2，
- x(−2) = 3，
- x(−1) = 0，
- x(0) = −1，
- x(1) = 2，
- x(2) = 3，
- x(3) = 1
該離散時間訊號可以用下圖所示的圖形表示。
離散時間訊號的函式表示
在離散時間訊號的函式表示中，訊號的幅值寫在n的值旁邊。因此，上述離散時間訊號x(n)可以用如下所示的函式表示：
$$\mathrm{x(n)=\left\{\begin{matrix} -2\: for \: n=-3\ 3\: for \: n=-2\ 0 \: for \: n=-1\ -1 \: for\:n=0\ 2\:for\:n=1\ 3\:for\:n=2\ 1\:for\:n=3\ \end{matrix}\right.}$$
離散時間訊號的表格表示
在離散時間訊號的表格表示中，取樣時刻n和在對應取樣時刻的離散時間訊號的幅值以表格的形式表示。上述離散時間訊號x(n)可以用下表表示：
| n | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| x(n) | -2 | 3 | 0 | -1 | 2 | 3 | 1 |
離散時間訊號的序列表示
離散時間訊號x(n)可以用如下序列表示：
$$\mathrm{x(n)=\begin{Bmatrix} -2,3,0,-1,2,3,1\ \uparrow \ \end{Bmatrix}}$$
這裡，箭頭標記(↑)表示對應於n = 0的項。當在離散時間訊號的序列表示中沒有指示箭頭時，則序列的第一項對應於n = 0。
離散時間序列的和與積
兩個離散時間序列的和是透過將序列的對應元素相加得到的，即：
$$\mathrm{\left \{ C_{n} \right \}=\left \{ a_{n} \right \}+\left \{ b_{n} \right \}\; \rightarrow \; C_{n}=a_{n}+b_{n}}$$兩個離散時間序列的積是透過將序列的對應元素相乘得到的，即：
$$\mathrm{\left \{ C_{n} \right \}=\left \{ a_{n} \right \}\left \{ b_{n} \right \}\; \rightarrow \; C_{n}=a_{n}b_{n}}$$序列和常數k的積是透過將序列的每個元素乘以該常數得到的，即：
$$\mathrm{\left \{ C_{n} \right \}=k\left \{ a_{n} \right \} \rightarrow \; C_{n}=ka_{n}}$$
更新於：2021年11月10日
14K+ 次瀏覽
廣告