資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學在數軸上表示$\sqrt{3.5},\sqrt{9.4}$和$\sqrt{10.5}$。
已知：
已知數為$\sqrt{3.5},\sqrt{9.4}$和$\sqrt{10.5}$
要求：
我們需要在數軸上表示$\sqrt{3.5},\sqrt{9.4}$和$\sqrt{10.5}$。
解:
1. 畫一條線段$AB=3.5$單位長度。
2. 將$B$延長到點$C$，使得$BC=1$單位長度。
3. 找到$AC$的中點，設為$O$。
4. 以$O$為圓心，畫一個經過$A$和$C$的半圓。
5. 畫一條經過$B$且垂直於$OB$的直線，與半圓相交於$D$。
6. 以$B$為圓心，$BD$為半徑畫弧，交延長線$OC$於$E$。
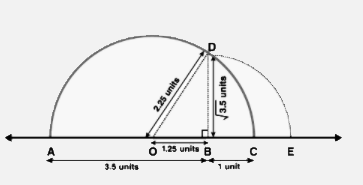
在直角三角形$OBD$中，
根據勾股定理，
$\mathrm{BD}^{2}=\mathrm{OD}^{2}-\mathrm{OB}^{2}$
$=O C^{2}-(O C-B C)^{2}$ [因為$\mathrm{OD}=\mathrm{OC}$]
$\mathrm{BD}^{2}=2 \mathrm{OC} \times \mathrm{BC}-(\mathrm{BC})^{2}$
$=2 \times 2.25 \times 1-1$
$=3.5$
$\Rightarrow \mathrm{BD}=\sqrt{3.5}$
1. 畫一條線段$AB=9.4$單位長度。
按照上述步驟2到6進行操作。
$\mathrm{BD}^{2}=2 \mathrm{OC} \times \mathrm{BC}-(\mathrm{BC})^{2}$
$=2 \times 5.2 \times 1-1$
$=9.4$
$\Rightarrow \mathrm{BD}=\sqrt{9.4}$
1. 畫一條線段$AB=10.5$單位長度。
按照上述步驟2到6進行操作。
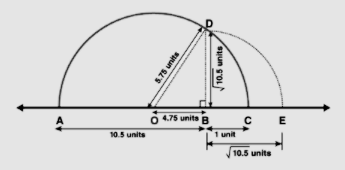
$\mathrm{BD}^{2}=2 \mathrm{OC} \times \mathrm{BC}-(\mathrm{BC})^{2}$
$=2 \times 5.75 \times 1-1$
$=10.5$
$\Rightarrow \mathrm{BD}=\sqrt{10.5}$
68 次瀏覽
