在數軸上表示$\sqrt{5}$。

已知

已知數為$\sqrt{5}$。

要求

我們需要在數軸上表示$\sqrt{5}$。

解答

為了解答這個問題，我們應該使用勾股定理。

斜邊² = 底邊² + 高²

• 首先畫一條數軸，標出'0'、'1'和'2'。
• 以1個單位長度為邊長，從'2'點作一條垂直於數軸的線段。
• 連線(0)點和新線段的端點。
• 這樣就構成了一個直角三角形。
• 我們把這個三角形命名為ABC，其中BC是高(垂直邊)，AB是三角形的底邊，AC是直角三角形ABC的斜邊。

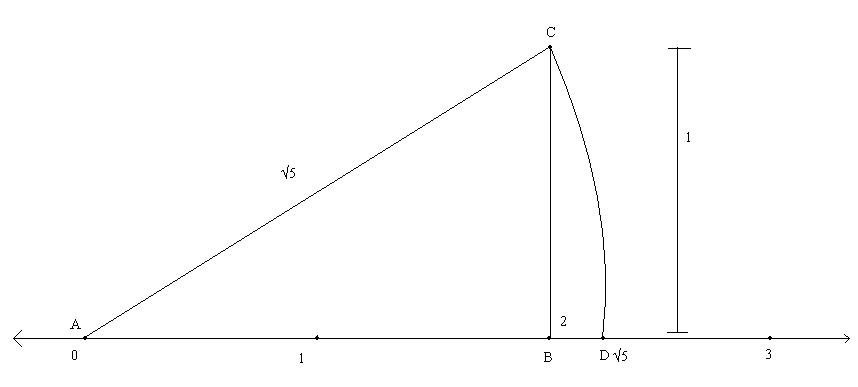
我們知道，$AC^2 = 2^2 + 1^2$

                    $AC^2 = 4+1 = 5$

                    $AC = \sqrt{5}$

AC2=22+12AC²=2²+1²

AC2=22+12AC²=2²+1²AC²=2²+1²

Tutorialspoint

更新於：2022年10月10日

瀏覽量：50

開啟你的職業生涯

完成課程獲得認證

開始學習