在數軸上表示$\sqrt{6},\ \sqrt{7},\ \sqrt{8}$。

已知：數$\sqrt{6},\ \sqrt{7},\ \sqrt{8}$。

要求：在數軸上表示$\sqrt{6},\ \sqrt{7},\ \sqrt{8}$。

解

1. 畫一條數軸。

2. 在數軸上標記一點A，使得$OA=2$個單位。

3. 取$AP=1$個單位。

4. 應用勾股定理，

$OP^2=OA^2+AP^2=2^2+1^2=4+1=5$個單位

$\Rightarrow OP=\sqrt{5}$

5. 以O為圓心，以半徑$r=OP$畫弧。該弧與數軸相交於點B。

$OB=OP=\sqrt{5}$。

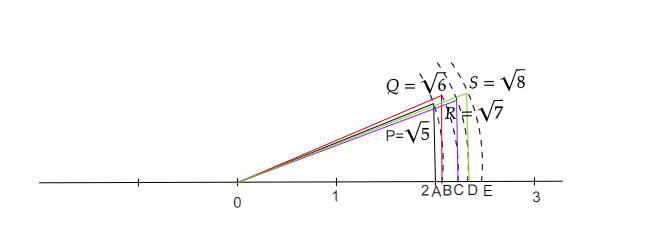
6. 取$BQ=1$個單位，$OB=\sqrt{5}$。

$\Rightarrow OQ^2=OB^2+BQ^2=(\sqrt{5})^2+1^2=5+1$

$\Rightarrow OQ=\sqrt{6}$

7. 以半徑$r=OQ$畫弧，該弧與數軸相交於點C。則$OC=\sqrt{6}$

8. 同理，在數軸上畫出點D和E。

因此，點$C=\sqrt{6}$，$D=\sqrt{7}$，$E=\sqrt{8}$是數軸上所需標記的點。

教程點

更新於：2022年10月10日

瀏覽量：375

開啟你的職業生涯

完成課程獲得認證

開始學習