證明外接於圓內接矩形ABCD的圓心是其對角線的交點。

待辦事項

我們必須證明外接於圓內接矩形ABCD的圓心是其對角線的交點。

解答

ABCD是一個圓內接矩形，對角線AC和BD相交於O點。

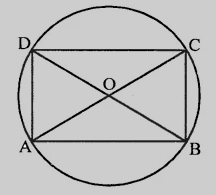
設O為外接於矩形ABCD的圓的圓心。

矩形的每個角都是直角，AC是圓的弦。

因此，

AC是圓的直徑。

類似地，我們可以證明對角線BD也是圓的直徑。

這意味著，

圓的直徑經過圓心。

因此，矩形對角線的交點是圓的圓心。

教程點

更新於: 2022年10月10日

135次瀏覽

開啟您的職業生涯

完成課程獲得認證

開始學習