如果圓內接四邊形的對角線是過四邊形頂點的圓的直徑，證明該四邊形是矩形。

已知

圓內接四邊形的對角線是過四邊形頂點的圓的直徑。

要求

我們必須證明它是一個矩形。

解答

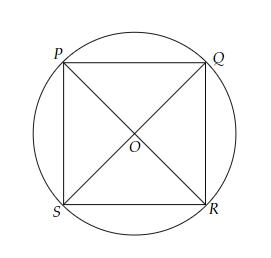
設 $PR$ 和 $QS$ 是圓內接四邊形 $PQRS$ 的對角線。

這意味著，

$PR$ 和 $QS$ 是圓的直徑。

$PR=QS$

$OP=OQ=OR=OS$    (圓的半徑)

四邊形 $PQRS$ 的對角線相等且互相平分。

因此，四邊形 $PQRS$ 是一個矩形。

證畢。

教程點

更新於: 2022年10月10日

264 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始學習