證明圓內接四邊形的各邊的垂直平分線共點。

待辦事項

我們需要證明圓內接四邊形的各邊的垂直平分線共點。

解答

設 $ABCD$ 是一個圓內接四邊形。

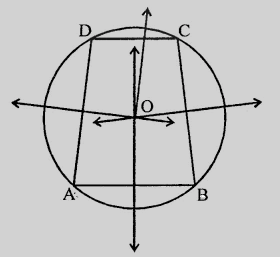
我們知道，

圓內接四邊形的每一條邊都是圓的弦，並且弦的垂直平分線過圓心。

因此，

每條邊的垂直平分線都將經過圓心 $O$。

因此，圓內接四邊形的各邊的垂直平分線共點。

教程點

更新於: 2022年10月10日

848 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始學習