如果圓內接四邊形的一對對邊相等，證明其對角線也相等。

已知

圓內接四邊形的一對對邊相等。

要求

我們必須證明其對角線相等。

解答

設圓內接四邊形 $ABCD$ 中，$AB = CD$，$AC$ 和 $BD$ 是對角線。

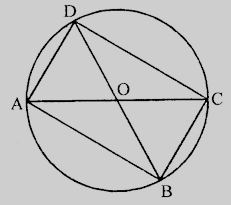
$AB = CD$

弧 $AB =$ 弧 $CD$

在兩邊加上弧 $BC$，得到：

弧 $AB +$ 弧 $BC =$ 弧 $BC +$ 弧 $CD$

弧 $AC =$ 弧 $BD$

因此，

$AC = BD$

因此，圓內接四邊形的對角線相等。

教程點

更新於： 2022 年 10 月 10 日

54 次檢視

開啟你的 職業生涯

完成課程獲得認證

立即開始