證明在直角三角形中，斜邊的平方等於其他兩條邊的平方和。

已知： 直角三角形ABC，其中∠B=90°

求證： (斜邊)² = (底邊)² + (高)²

或者

在△ABC中： AC² = AB² + BC²

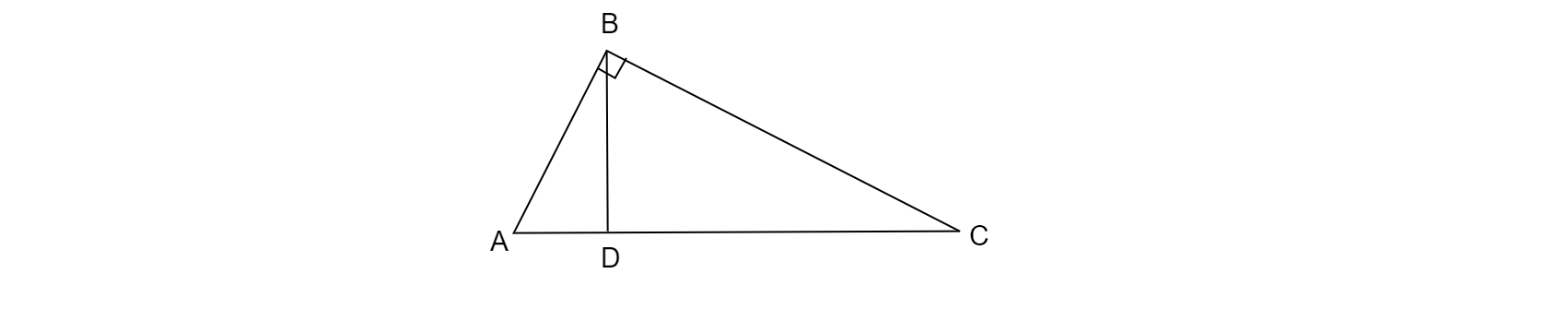
作圖： 從B點作BD⊥AC。

在三角形△ADB和△ABC中，

我們有

∠ADB = ∠ABC [均等於90°]

且，∠A = ∠A [公共角]

因此，根據AA相似準則，我們有

△ADB ~ △ABC

AD/AB = AB/AC [在相似三角形中，對應邊成比例]

                                                           

AB² = AD × AC .......(1)

在三角形△BDC和△ABC中，我們有

∠CDB = ∠ABC [均等於90°]

且，∠C = ∠C [公共角]

因此，根據AA相似準則，我們有

△BDC ~ △ABC

⇒ DC/BC = BC/AC [在相似三角形中，對應邊成比例]

⇒ BC² = AC × DC .......(2)

將公式(1)和(2)相加，我們得到

AB² + BC² = AD × AC + AC × DC

⇒ AB² + BC² = AC(AD + DC)

⇒ AB² + BC² = AC × AC = AC²

⇒ AB² + BC² = AC²

因此，證明了AB² + BC² = AC²