資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法學證明平行四邊形的對角線將其分成兩個全等三角形。
已知
平行四邊形的對角線將其分成兩個全等三角形。
需要證明
我們需要證明平行四邊形的對角線將其分成兩個全等三角形。
解答
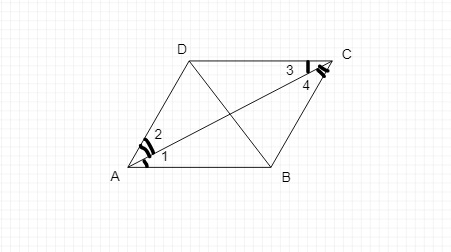
取平行四邊形ABCD，連線其任意兩個不相鄰的頂點，例如A和C。
在平行四邊形ABCD中，BC平行於AD，AB平行於DC。
AC是平行線BC和AD的截線，也是平行線AB和DC的截線。
設由這些平行線和截線形成的角為角1、2、3和4。
考慮△ABC和△CDA，
∠1 = ∠3 (因為內錯角相等)
∠2 = ∠4 (因為內錯角相等)
AC = CA (公共邊)
因此，根據ASA定理，△ABC ≅ △CDA。
因此，對角線AC將平行四邊形ABCD分成兩個全等三角形ABC和CDA。
證畢。
更新於：2022年10月10日
828 次瀏覽
廣告