你在九年級學過，三角形的中線將其分成兩個面積相等的三角形。驗證一下頂點為 $A (4, -6), B (3, -2)$ 和 $C (5, 2)$ 的 $∆ABC$ 的結果。

已知

三角形的頂點為 $A (4, -6), B (3, -2)$ 和 $C (5, 2)$。

操作

我們需要證明三角形的中線將其分成兩個面積相等的三角形。

解答

設 $A (4, -6), B (3, -2)$ 和 $C (5, 2)$ 為三角形 $ABC$ 的頂點。

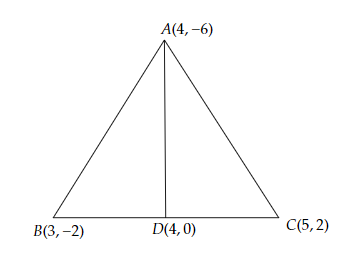
設 $D$ 為 $\triangle ABC$ 的邊 $BC$ 的中點。 

這意味著，

點 $D$ 的座標 = BC 的中點 $= (\frac{3+5}{2}, \frac{-2+2}{2})$

$=(\frac{8}{2}, 0)$

$=(4, 0)$

$AD$ 是 $\triangle ABC$ 的中線。

$\triangle \mathrm{ABD}$ 的面積 $=\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$

$=\frac{1}{2}[4 \times(-2-0)+3(0+6)+4(-6+2)]$

$=\frac{1}{2}[-8+18-16]$

$=\frac{-6}{2}$

$=3$ 平方單位 

$\triangle \mathrm{ADC}$ 的面積 $=\frac{1}{2}[4(0-2)+4(2+6)+5\times(-6-0)]$

$=\frac{1}{2}[-8+32-30]$

$=\frac{-6}{2}$

$=3$ 平方單位

$\triangle \mathrm{ABD}$ 的面積 = $\triangle \mathrm{ADC}$ 的面積

因此，三角形的中線將其分成兩個面積相等的三角形。

教程點

更新於: 2022 年 10 月 10 日

27 次瀏覽

開啟你的 職業生涯

完成課程獲得認證

開始學習