在下圖中，$OA=5\ cm，AB=8\ cm$，且$OC$垂直於$AB$，求$CD$的值。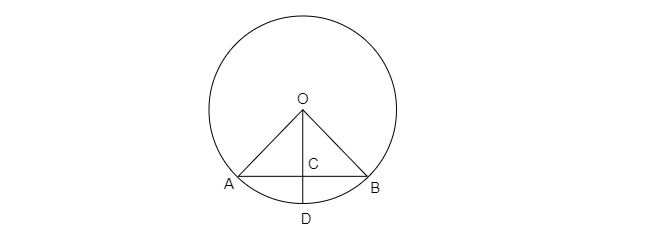

已知：圖中$OA=5\ cm，AB=8\ cm$，且$OC$垂直於$AB$。

求解：求$CD$的值。

解

已知$OA=5\ cm$

$AB=8\ cm$

$\because AB$為弦，且$OC$垂直於$AB$。

因此$OC$平分$AB$。

$\Rightarrow AC=\frac{AB}{2}$

$\Rightarrow AC=\frac{8}{2}$

$\Rightarrow AC=4\ cm$

在直角三角形$\vartriangle OAC$中，

$OA^2=OC^2+AC^2$                                  [勾股定理]

$\Rightarrow OC^2=OA^2-AC^2$

$\Rightarrow OC^2=5^2-4^2$

$\Rightarrow OC^2=25-16$

$\Rightarrow OC^2=9$

$\Rightarrow OC=\sqrt{9}$

$\Rightarrow OC=3\ cm$

我們知道$CD=OD-OC$

$\Rightarrow CD=5-3$                          [$\because OD=OA=5\ cm=半徑$]

$\Rightarrow CD=2\ cm$

因此，$CD=2\ cm$

Tutorialspoint

更新於：2022年10月10日

42 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習